Bli ferdig med kapittel 5 (fundamentalteoremet for kalkulus, arealberegninger, numerisk integrasjon), og avsnitt 9.8 om uekte integraler.
Riemannsummer og integrerbarhet, spesielt integrerbarhet av monotone funksjoner og kontinuerlige funksjoner (der det første er enklere enn det siste). Jeg viste et eksempel på en ikke-integrerbar funksjon: Den som er 0 i alle irrasjonale punkter og 1 i alle rasjonale punkter.
Transparenten jeg brukte i forelesningen (også ps, pdf).
Klarer du vise at Johann Peter Gustav Lejeune Dirichlets funksjon er integrerbar? (Oppgaven finnes også som ps og pdf. Ingen av førsteklassingene på data har klart den!)
Første timen for jeg over mange temaer med en harelabb: Litt om middelverdi for integraler (5.6), litt om substitusjon i bestemte integraler (5.7; jeg hadde alt dekket substitusjon i ubestemte integraler), litt om arealberegninger (5.8) og litt om uekte integraler (9.8). Det ble jo litt springende og usammenhengende, men jeg vet ikke riktig hvordan jeg kunne unngått det.
Andre timen var viet til numerisk integrasjon (5.9): Først og fremst midtpunktmetoden, trapesmetoden og Thomas Simpsons metode, alle med tilhørende feilestimater. Jeg sa til og med noen ord om hvor feilestimatet for midtpunktmetoden kommer fra, og regnet et eksempel for å vise hvordan det kan brukes i praksis for å vite hvor mange deleintevaller man skal bruke for å få ønsket nøyaktighet. Ett poeng som jeg håper kom klart frem, er at feilestimatet er et estimat, og som sådan er det ikke alltid nødvendig å finne den beste verdien på konstanten K2 eller K4. Feilestimatet for Simpson kom litt hesblesende i timens siste minutter.
Jeg skulle ønske jeg hadde hatt tid til å si noen ord om det at midtpunktmetoden og trapesmetoden begge gir eksakt rett svar om integranden er lineær, mens Simpsons metode er den entydige kombinasjonen av de to som i tillegg er eksakt riktig for en kvadratisk integrand. Kanskje i neste uke, om jeg føler at det er tid. (Det ble ikke det.)
Om å sette opp integralformler, og hvordan komme fra Riemannsummer til integraler (avsnitt 6.1). For eksempel når noe akkumuleres over tid. Dernest Bonaventura Francesco Cavalieris prinsipp (fra avsnitt 6.2), eller kunsten å beregne volumer ved å integrere et tverrsnitt. Som eksempel viste jeg formelen A=Gh/3 for en kjegle med vilkårlig fasong på grunnflaten (en pyramide er for eksempel en kjegle med kvadratisk grunnflate). Deretter om anvendelsen av Cavalieris prinsipp på rotasjonslegemer. Til sist nevnte jeg raskt hvordan man også kan bruke metoden med sylinderskall (fra avsnitt 6.3) til å beregne volum for rotasjonslegemer.
Først et raskt eksempel på en volumberegning ved sylinderskallmetoden, så var resten av tiden viet til avsnitt 6.4.
Først definerte jeg buelengde L(C) for en kurve C som en minste øvre grense for lengden av den brukne linjen man får ved å velge et endelig antall punkter i rekkefølge langs linjen, og så trekke linjestykker mellom dem. Så beviste jeg formelen for buelengden beregnet ut fra den deriverte, under forutsetningen at det involverte integralet eksisterer. Etter et eksempel gikk jeg over til å se på arealet av rotasjonsflater, hvor jeg var adskillig mindre rigorøs men forhåpentlig klarte å formidle hovedprinsippet for hvordan slike arealer beregnes. Etter et par eksempler avsluttet jeg timen med å bruke noen minutter på å vise hvordan Maple kan brukes til å visualisere rotasjonsflater.
Resten av kapittel 6 (6.5-6.6): Separable differensialligninger, kraft og arbeid.
Deretter kapittel 7 om eksponensial- og logaritmefunksjonene.
For meg var dette en dårlig uke, på grunn av en forkjølelse. Dette har ikke bare påvirket stemmen, men jeg tror jeg gjorde flere feil i forelesningene enn jeg pleier.
Avsnitt 6.5: Først litt om førsteordens differensialligninger generelt. Normalt (det vil si om høyresiden er tilstrekkelig «snill») har initialverdiproblemet for en førsteordens differensialligning en entydig løsning i en omegn om punktet hvor initialbetingelsen var gitt, selv om det i praksis kan være vanskelig å finne en formel for løsningen. Å integrere, det vil si å finne en antiderivert til en funksjon f, er det samme som å løse differensialligningen y'=f(x). Å tegne opp retningsfelt for en differensialligning y=F(x,y) er et nyttig verktøy for å gi en kvalitativ forståelse av løsningene.
Kan du integrere, kan du i prinsipp også løse den separable differensialligningen f(y)y'=g(x) ved formelt å skrive y'=dy/dx, multiplisere formelt med dx og integrere ligningen f(y)dy=g(x)dx. Den generelle løsningen er gitt ved F(y)=G(x) der F'=f og G'=g, og alt som gjenstår er å løse denne ligningen med hensyn på y (det kan være vanskelig nok).
Jeg regnet et par enkle eksempler, ett som viser at løsningen kan divergere mot uendelig innenfor en endelig avstand fra initialpunktet, og ett som viser at initialverdiproblemet ikke nødvendigvis har bare en løsning dersom høyresiden har en ubegrenset derivert.
Jeg regnet også et par eksempler hvor poenget var både å illustrere hvordan man stiller opp en differensialligning for et problem og hvordan man løser differensialligningen. Jeg så på den vanligste populasjonsmodellen (eksponensiell vekst), kritiserte modellen på side 401-402, og regnet i stedet litt på den logistiske populasjonsmodellen P'=kP(Pmax-P).
Flere eksempler på å stille opp og løse differensialligninger: Et designproblem for en (høy) betongsøyle, og tømming av kar der strømningen ut av et hull er gitt ved Evangelista Torricellis lov.
Avsnitt 7.1-7.4 er ment som selvstudium, men jeg sa noen ord om hvordan det faller naturlig å definere eksponensialfunksjonen exp ved en differensialligning, ln som integralet som opptrer i løsningen (den inverse til exp), og hvordan dette gir alle de nødvendige egenskapene til den generelle eksponensialfunksjonen ax i ett slag, uten at det er nødvendig å diskutere tilfellet med rasjonale eksponenter separat.
Til slutt litt raskt (fra 7.5) om eksponensiell vekst og nedbrytning, med en rask introduksjon til karbondatering.
Logaritmene ble oppfunnet av John Napier på begynnelsen av 1600-tallet, men ikke i en form som vi ville gjenkjent i dag (spesielt var ikke Napiers logaritme beregnet i 1 lik 0, slik vi er vant til det). I stedet ble det Henry Briggs som (i diskusjon med Napier) utviklet det som den dag i dag er kjent som den Briggske logaritme, det vil si log10.
Kanskje litt fra avsnitt 7.6 om lineære førsteordens differensialligninger med konstante koeffisienter, før vi går løs på kapittel 11 om følger og rekker.
Fra avsnitt 11.3 om følger. Jeg definerte en følge som en funksjon definert på de naturlig tall {1,2,3,...} (eller {0,1,2,3,...}, eller for den saks skyld {m,m+1,m+2,...} der m er et eller annet naturlig tall). Men til forskjell fra andre funksjoner foretrekker vi å skrive an i stedet for a(n). Jeg definerte konvergens og grense for følger helt analogt med grensen til en funksjon f(x) når x går mot uendelig. Vi har de opplagte enkle lovene om grense av summer, produkter og kvotienter, og en substitusjonslov om grensen av {f(an) - som også har åpenbare versjoner ut over den boka nevner, dersom følgen divergerer mot pluss eller minus uendelig og funksjonen har en (endelig eller uendelig) grense der. Endelig har vi skviseloven, som virker like bra for følger som for funksjoner.
Langt mindre opplagt er kompletthetsaksiomet for de reelle tall, som sier at enhver monoton følge av reelle tall enten konvergerer, eller divergerer mot pluss eller minus uendelig. Men etter at jeg hadde introdusert dette aksiomet var timen slutt.
Det virker kanskje rart at jeg snakker om kompletthetsaksiomet, for aksiomer er da noe man betrakter som så opplagt at det ikke trenger noe bevis? Nei, det er ikke så enkelt. Det er riktig at matematikken i bunn og grunn er basert på aksiomer som kan virke opplagte, eller som i det minste er så grunnleggende at de er bortimot umulige å bevise på grunnlag av noe enda mer grunnleggende. Men ordet aksiom har også en annen betydning: Vi snakker gjerne om en aksiomatisk beskrivelse av et objekt dersom vi har en liste av egenskaper som til sammen definerer objektets struktur entydig. Mest berømt er kanskje Guiseppe Peanos aksiomer for de naturlige tall. Til tross for en slik aksiomatisk beskrivelse av de naturlige tallene kan disse defineres ut fra mer grunnleggende begreper (vanligvis mengdelære, men lambda-kalkyle har og vært brukt). På samme måte har vi en aksiomatisk beskrivelse av de reelle tall, der kompletthetsaksiomet inngår som ett av aksiomene. De andre aksiomene er alle de vanlige reglene for de fire regningsartene, pluss ordningen av de reelle tallene (slik at x2>0 for alle x unntatt 0) og Arkimedesaksiomet, som fastslår at det for ethvert reelt tall finnes et naturlig tall som er større. (Det opprinnelige aksiomet til Arkimedes) var nok geometrisk av natur: Gitt to linjestykker, kan du alltid ved å legge tilstrekkelig mange kopier av det korteste linjestykket etter hverandre overstige lengden på det lengste av dem.) En fordel ved å ha en aksiomatisk beskrivelse av de reelle tallene er at man så kan velge en av mange forskjellige, men i siste instans ekvivalente, metoder for å konstruere de reelle tallene. De konstrueres vanligvis ut fra følger av rasjonale tall - man kan for eksempel starte med alle monotone, begrensede følger av rasjonale tall og så slå sammen to slike følger dersom tallene i de to følgene kommer vilkårlig nær hverandre når man kommer langt ut i følgene.
Unnskyld hvis dette ble for langt - jeg kunne ikke motstå fristelsen til å bable i vei her, for dette er etter min mening det mest sentrale punktet i hele dette kurset, selv om det gjerne tar en del tid (kanskje flere år) å innse det.
Jeg startet med å gjenta kompletthetsaksiomet, og belyste det ved to eksempler. Først et alternativt bevis for at {rn} konvergerer mot 0 dersom 0<<r<1: Følgen er opplagt monotont avtagende, og kan ikke divergere mot minus uendelig - så den har en grense L. Går vi til grensen i rekursjonsrelasjonen rn+1=rrn finner vi L=rL, hvorav L=0.
Dernest ga jeg et konvergensbevis for Newtons metode, basert på en naturlig antagelse om konveksitet. Endelig fastslo jeg det (nesten almengyldige) prinsipp at: Ethvert teorem som påstår at noe konvergerer, uten å spesifisere grensen, bygger i siste instans på kompletthetsaksiomet. Eksempler er teoremene om eksistens av integralet for kontinuerlige eller monotone funksjoner (integralet er jo en grense av Riemannsummer), og skjæringssetningen (som ikke sier noe om konvergens, men beviset bygger på konvergens, og teoremet ender ganske riktig i en uspesifisert størrelse).
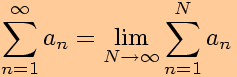
Avsnitt 11.3, om rekker, kan veldig kort og brutalt oppsummeres ved formelen til høyre. Det er en liten håndfull rekker vi noenlunde enkelt kan behandle manuelt, nemlig geometriske rekker, den harmoniske rekken, og alle rekker hvor n-te ledd ikke går mot null (slike rekker er alltid divergente).
Avsnitt 11.4 er viet Brook Taylor, eller rettere sagt rekkene og polynomene hans. Taylorpolynomet av n-te orden i x=a til en funksjon f(x) er det n-tegradspolynomet som har samme deriverte som f i punktet x=a opp til n-te orden. Jeg utledet formelen bare for a=0, og skrev om Taylors formel, med restledd og det hele for dette tilfellet. Til slutt viste jeg fram noen plott av velkjente funksjoner og deres Taylorpolynomer ved hjelp av Maple. (Mapledokumentet jeg brukte i forelesningen finnes på nett i lett modifisert utgave.)