Fra avsnitt 13.7 gjenstår spesielt implisitt partiellderivasjon. Resten av tiden går med til 13.10 (annenderivert-testen) og 13.8 (retningsderiverte og gradientvektoren).
Fra avsnitt 13.7, om implisitt partiellderivasjon: Grunnidéen er presis den samme som for implisitt derivasjon for funksjoner av en variabel. Dersom funksjoner F og f er slik at for eksempel F(x,y,f(x,y))=0, kan vi finne de partiellderiverte av f ved å derivere identiteten med hensyn på x og y og så løse den resulterende ligningen. Dersom det krever divisjon med null, har vi åpenbart et problem. Men ellers garanterer implisitt funksjonsteoremet (ikke pensum) at ligningen definerer f implisitt i en omegn om et gitt punkt, forutsatt at f har kontinuerlige partiellderiverte.
Deretter avsnitt 13.8 om retningsderiverte og gradientvektoren. I motsetning til boka tok jeg utgangspunkt i kjerneregelen og differensialetog skrev dem på vektorform som en motivasjon. Gradientvektorens roller som normalvektor til tangentplanet og en peker i den retningen funksjonsverdien vokser raskest er også viktige. Husk også at et kritisk punkt er et punkt hvor gradienten er null eller ikke eksisterer. (Bemerkningen nederst side 856 og øverst side 857 utgår.)
Maple-regnearket fra forelesningen er tilgjengelig.
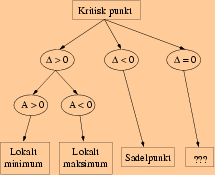
Avslutningen på avsnitt 13.8 (se over; jeg husker ikke lenger presis hvor tirsdagsforelesningen sluttet og torsdagsforelesningen startet.) Deretter 13.10 om annenderiverttesten for lokale minimum, maksimum og sadelpunkter. Jeg presenterte testen og regnet noen eksempler, men sa ikke et kløyva ord om hvorfor testen fungerer. (To gangers derivasjon langs rette linjer gjennom det kritiske punktet, koblet med en god forståelse for løsningen av annengradsligninger, er et godt utgangspunkt for forståelse. Se for øvrig «Discussion of Theorem 1» fra nederst side 877.)
Maple-regnearket fra forelesningen er tilgjengelig.
Avsnitt 13.9 (optimering med bibetingelser, Lagrangemultiplikatorer) og 14.1-14.2 (dobbeltintegraler).
Dagen ble viet avsnitt 13.9, om Joseph-Louis Lagranges multiplikatormetode for å finne ekstrempunkter med gitte føringer. Jeg forsøkte å rettferdiggjøre metoden geometrisk, ga et nestenbevis for metodens gyldighet (for en bibetingelse i to variable) og regnet en del eksempler. Litt terminologi: Jeg bruker ordene bibetingelse og føring om hverandre om samme sak, nemlig en ligning (muligens en av flere) som beskriver flaten eller kurven vi optimerer en funksjon over.
Maple-regnearket fra forelesningen er tilgjengelig.
Jeg gjorde meg ferdig med Lagranges metode for tre variable: Først en geometrisk forklaring på hvorfor den fungerer for en føring, deretter det samme for to føringer, etterfulgt av et eksempel på det siste.
Deretter startet jeg med dobbeltintegralet: Først over rektangler (avsnitt 14.1): Først definisjonen med Riemannsummer, så bemerket jeg at om vi summerer smårektanglene enten rekkevis eller kolonnevis blir den innerste summen en Riemannsum for et endimensjonalt integral - og om vi tar en kjapp en og erstatter den summen med integralet, blir den ytterste summen også en Riemannsum for et integral: Formelen for iterert integrasjon er født. Etter et eksempel på integrasjon over et rektangel viste jeg til slutt hvordan man integrerer xy2 over trekanten med hjørner i (0,0), (1,0) og (1,1): Begge de itererte integralene ga samme sum (svaret var 1/15). Den teoretiske begrunnelsen for fremgangsmåten og flere eksempler får vente til neste uke.
Vi har nettopp rundet en viktig milepæl: Vi er ferdige med derivasjon og anvendelser av derivasjon og har startet med integrasjon. I ukene som kommer skal vi jobbe med integrasjon i to og tre variabler, over mer eller mindre kompliserte områder i to og tre dimensjoner og over flater i tre dimensjoner.
I denne uken skal vi bli ferdig med 14.2 (integrasjon over mer generelle områder i planet), 14.3 (areal- og volumberegninger ved dobbelintegral), 14.4 (dobbeltintegral i polarkoordinater, og 14.5 (anvendelser av dobbeltintegraler). Nesten fire avsnitt kan virke mye, men det er ikke mye teori i hvert avsnitt. Derimot er det mange praktiske ferdigheter å lære seg, så dere får nok å gjøre.
(tirsdag)
Avsnitt 14.2 om dobbeltintegrasjon over generelle områder i planet: Det viktigste eksistensteoremet er at dobbeltintegralet av en funksjon f over et område R er garantert å eksistere dersom:
At en lukket, begrenset mengde B i planet har null areal betyr dette: Tenk deg at B er inneholdt i et rektangel S i planet, med sider parallelle med aksene. For hver partisjon Q av S adderer vi opp arealene til de delrektanglene i Q som inneholder en bit av B. Dersom summen av disse arealene går mot null når normen |Q| til partisjonen går mot null, har B null areal.
Det lar seg gjøre å konstruere et eksempel på en enkel kurve i planet med positivt areal! Men heldigvis er det slik at enhver kurve som kan skrives på formen y=g(x) med en kontinuerlig g, eller x=h(y) med en kontinuerlig h, har null areal.
Dersom området R er horisontalt enkelt eller vertikalt enkelt kan vi alltid integrere over R ved et iterert integral, hvor grensene i det innerste integralet avhenger av integrasjonsvariabelen i det ytterste. Dette kan også brukes «i revers» for å bytte om integrasjonsrekkefølgen: Hvis du har gitt et iterert integral må du bestemme området R og deretter skrive integralet i motsatt rekkefølge. Det kan hende du må dele opp området først, for å få det til å være (horisontalt eller vertikalt) enkelt.
Maple-regnearket fra forelesningen er tilgjengelig.
Avsnitt 14.4: Dobbeltintegrasjon i polarkoordinater. Du må aldri glemme den ekstra faktoren r når du skifter fra rektangulære til polarkoordinater! Formelen motiveres ved å lage en Riemannsum for integralet ved å dele opp området i «polare rektangler» i stedet for vanlige rektangler. Jeg regnet oppgave 14.3.42 med polarkoordinater for integralet (se også slutten av Maple-regnearket fra tirsdag). Jeg integrerte også x2+y2 over sirkelen (x-1)2+y2=1. (Dette hadde sikkert gått enklere med polarkoordinater med origo i sentrum i sirkelen.) Og så regnet jeg eksempel 5, om det berømte integralet av exp(-x2). Boken prøver å gjøre det rigorøst ved å integrere over endelige kvadrater og sirkelskiver og så la disse vokse mot uendelig, men jeg syntes ikke det var videre overbevisende - så jeg bare regnet med uendelige grenser i utgangspunktet, som gjør hele regnestykket lettere å forstå.
Avsnitt 14.5: Anvendelser av dobbeltintegralet. Her nådde jeg bare så vidt å rettferdiggjøre integralformlene for masse og massesenter for en tynn plate, og å forklare det første teoremet til Pappus fra Alexandria. (Det er forresten interessant at biografien ikke nevner de to teoremene vi kjenner som Pappus teoremer.)
Denne uken blir det trippelintegraler: i kartesiske koordinater (avsnitt 14.6) og sylinder- og kulekoordinater (14.7).
Først noen ord om det som gjensto av avsnitt 14.5 om de to Pappus-teoremene.
Resten av tiden gikk med til avsnitt 14.6, trippelintegraler. Det er overhode ingen teoretiske overraskelser her, så tiden går mest med på å se hvordan vi beregner trippelintegraler i praksis. Det som i praksis faller vanskeligst for de fleste, er å få innsikt i hvordan et legeme ser ut, når det er gitt ved ligninger for grenseflatene til legemet. Når det er gjort, er neste hinder å bestemme en passe integrasjonsrekkefølge og så finne grensene i hvert integral. I trippelintegraler er det seks mulige integrasjonsrekkefølger, så det er ofte vanskelig å velge! Etter å ha sagt litt om hvordan Riemannsummer kan lede til itererte integraler tok jeg et moderat komplisert eksempel: Volum og z-koordinaten til massesenteret for legemet begrenset av flatene z=1-x2, z=1-y2 og xy-planet. Se for øvrig Maple-regnearket fra forelesningen.
Jeg startet med å gå tilbake til det siste eksemplet fra tirsdag. Der kom vi fram til et integral som kan tolkes som et iterert integral med et enkeltintegral (over z) ytterst og et dobbeltintegral (over x og y) innerst, der dobbeltintegralet kan tolkes som et integral over et horisontalt snitt gjennom legemet T. Når integranden er konstanten 1, er dette Cavalieris prinsipp, så vi kan altså si vi har oppdaget en naturlig generalisering av dette prinsippet.
Deretter tok jeg fatt i avsnitt 14.7, om integrasjon i sylinder- og kulekoordinater. Når du har sett integrasjon i polarkoordinater, kommer det neppe som noen overraskelse at det også her dukker opp en ekstra faktor i trippelintegralet når det uttrykkes i nye koordinater. For øvrig er det ingen nye overraskelser, men utfordringen er å forstå geometrien godt nok til å kunne stille opp integralene og integrasjonsgrensene korrekt.
For z-enkle områder kan formelen for integrasjon i sylinderkoordinater oppfattes som vanlig integrasjon i z, etterfulgt av en evaluering av dobbeltintegralet som står igjen i polarkoordinater. Men formelen fungerer like godt for områder som ikke er z-enkle - vi må bare gjøre integrasjonsrekkefølgen annerledes. Som eksempel beregnet jeg volum og massesenter for et legeme begrenset av x2+y2-z2=1, z=1, z=-1 og x=0. Trippelintegralet jeg fikk kan tolkes som det generaliserte Cavilieris prinsipp, hvor vi bruker polarkoordinater for flateintegralet over tverrsnittet.
Jeg regnet også oppgave 14.7.25 i sylinderkoordinater. Deretter innførte jeg integralformelen for kulekoordinater og gjorde oppgaven igjen med kulekoordinater. Det ble enklere enn med sylinderkoordinater.
Harald Hanche-Olsen 2001-03-13 12:24:09 UTC