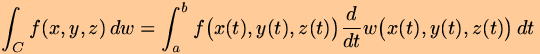
Mesteparten av tiden går med til flater på parameterform og beregning av overflateareal for slike. Til slutt starter vi på kapittel 15, nærmere bestemt 15.1 om vektorfelter: Gradientfelt, divergens og curl (også av og til kalt rotasjon).
Jeg avsluttet 14.7 ved å tegne og forklare om formelen for integrasjon i kulekoordinater. Underveis fikk vi nesten gratis en integrasjonsformel for arealet av et kuleskall. Jeg utførte integralet og fikk formelen vi er vant til. Dette ledet så naturlig til avsnitt 14.8 om arealberegninger: Dette ble nesten som for arealet av kuleskallet, bortsett fra at vi generelt ikke kan vente at de to tangentvektorene vi får står ortogonalt på hverandre. Dermed er det blir ikke flateelementet et tilnærmet rektangel, men et parallellogram i stedet. I stedet for å multiplisere lengdene av de to vektorene kan vi finne arealet av parallellogrammet ved å ta lengden av kryssproduktet. Resultatet blir integrasjonsformelen for flater på generell parametrisk form.
Som eksempel regnet jeg ut overflaten av en torus (og fikk samme svar som Pappus ga oss). Så gjorde jeg det samme for den delen av flaten z=xy som ligger innenfor sylinderen x2+y2=1, ved å bruke x og y som parametre. Jeg døpte dem om til u og v for å gjøre sammenhengen med det generelle tilfellet klar, men kommer neppe til å gjøre det i fremtiden. I løpet av det ene minuttet som var til overs fortalte jeg hvordan metoden greit generaliseres til arealberegninger for grafen til en funksjon (formel (9) side 943 i E&P).
Jeg forklarte litt mer om arealberegningsformelen for grafen til en funksjon av to variable, og spesielt hvordan den er en naturlig generalisering av formelen for lengden av grafen til en funksjon av en variabel (formel (2) side 390). Jeg utledet også arealformelen for grafen til en funksjon gitt i sylinderkoordinater, og viste at den kan tolkes som resultatet av å evaluere dobbeltintegralet for arealet i kartesiske koordinater ved hjelp av polarkoordinater.
Dermed starter vi på Kapittel 15, og starter med 15.1 om vektorfelter. Jeg viste noen eksempler (spesielt gradientfelter, som alle steder er ortogonale på nivåkurvene til funksjonen de er gradient til), fortalte litt om derivasjon av vektorfelter, og avsluttet med å motivere definisjonen av divergens i to dimensjoner. (Jeg beviste faktisk divergensteoremet for et rektangel i planet.) Maple-regnearket fra forelesningen er tilgjengelig.
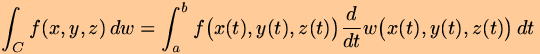
Avsnitt 15.2: kurveintegraler. Jeg tok en liten vri på fremstillingen i boka: Jeg definerte kurveintegralet på venstresiden i ligningen over for to funksjoner f og w begge definert på kurven C, først ved å konstruere Riemannsummer basert på en partisjon av C og så la denne bli finere og finere. Men om kurven er gitt ved en parametrisering kan jeg lage en slik partisjonering ved å dele opp parameterintervallet [a,b], og dersom w(x(t),y(t),z(t)) er differensiabel med hensyn på t kan vi bruke sekantsetningen for denne funksjonen på hvert delintervall og få en Riemannsum for integralet på høyresiden av ligningen over.
Tross denne litt abstrakte og generelle definisjonen, er vi i praksis bare interessert i et fåtall mulige valg for w: Nemlig buelengde s målt langs kurven, eller en av koordinatene x, y eller z. Kurveintegralet av et vektorfelt langs en kurve er et viktig spesialtilfellet, som kombinerer de siste tre valgene for w.
Avsnitt 15.3 handler om kurventigraler for vektorfelter. Fundamentalteoremet for kurveintegraler sier at kurveintegralet av gradienten til en funksjon f langs en kurve fra A til B er f(B)-f(A). Spesielt er integralet uavhengig av veien, og avhenger kun av endepunktene. Det viser seg at integralet er uavhengig av veien bare for vektorfelter som kan skrives som en gradient. Slike vektorfelt kalles konservative, og en funksjon f slik at gradienten til f er et gitt vektorfelt F kalles en potensialfunksjon for F. To potensialfunksjoner for samme vektorfelt har en konstant differanse - og har du en potensialfunksjon for F, kan du alltids lage en annen ved å legge til en konstant. Helt til slutt nådde jeg knapt å nevne den viktigste testen for om et vektorfelt er konservativt: Teorem 3 side 981. Jeg må nok ta litt om det neste uke.
Eksempler nevnt i forelesningen: Eksempel 3. Dessuten vektorfeltet F(x,y)=yi. Det tilhørende kurveintegralet er interessant fordi det kan brukes til å måle arealet til innsiden av en lukket kurve, som ligger bak konstruksjonen av planimeteret. Spesielt er dette vektorfeltet ikke konservativt, siden integralet av et konservativt vektorfelt rundt en lukket kurve må være null. Jeg tok også tyngdefeltet som eksempel - men pass på at i fysikken opererer man med motsatt fortegnskonvensjon av det man gjør i matematikken, fordi dette passer bedre sammen med energibegrepet.
En digresjon: Den universelle gravitasjonskonstanten oppgis gjerne med rundt fire siffer, men nylig er den målt med betydelig høyere nøyaktighet. Likevel er produktet MG for jorden kjent med mye høyere nøyaktighet enn de to faktorene hver for seg, siden jordens tyngdefelt kan måles med ekstremt høy presisjon ved satelittobservasjoner.
Jeg startet med å avslutte avsnitt 15.3 med teorem 3. Boken gjør det bare for vektorfelt på rektangler, men jeg gjorde det for de mest generelle områdene hvor teoremet er sant, nemlig enkeltsammenhengende områder. At et område R er enkeltsammenhengende betyr to ting: (1) Det er sammenhengende, det vil si at for hvilke som helst to punkter i R finnes en kurve i R fra det ene punktet til det andre, og (2) Det har ingen «huller», det vil si det finnes ingen lukket vei i R som går rundt noe punkt som ikke er i R. Den «riktige» versjonen av teorem 3 sier da at et kontinuerlig deriverbart vektorfelt på et enkeltsammenhengende område er konservativt hvis og bare hvis det oppfyller testen med de partiellderiverte (ligning (13) side 981).
Hvis feltet er konservativt blir ligning (13) ikke noe annet enn likhet av blandede partiellderiverte for potensialfunksjonen. Omvendt, om (13) holder vil Greens teorem fortelle at integralet av vektorfeltet rundt en enkel lukket kurve blir null, og det følger at integralet mellom to punkter er uavhengig av veien mellom punktene, slik at feltet er konservativt. (Dette argumentet har noen huller som krever en del jobb å fylle, men det overser vi her.)
Eksempel: F=(-yi+xj)/(x2+y2) er et felt som oppfyller betingelsen, men som ikke er konservativt i sitt definisjonsområde (planet med unntak av origo). Men om vi begrenser definisjonsområdet til hele planet med unntak av en halvlinje med ene endepunktet i origo, så blir feltet konservativt. En variant av dette eksemplet viser at teorem 3 aldri er sant for sammenhengende områder som ikke er enkeltsammenhengende, så teoremet er akkurat så sterkt som man kan håpe på.
Deretter avsnitt 15.4: George Greens teorem. Dette kan betraktes som et fundamentalteorem for dobbeltintegralet: Integralet av en derivert over et område er et uttrykk som bare involverer funksjonsverdier på randen av området. Dere har allerede støtt på to fundamentalteoremer: Først i envariabelanalysen og nå nylig for kurveintegraler. Alle varianter av fundamentalteoremet reduserer antall integraler med en.
Mer om Greens teorem: Det kan tolkes som et todimensjonalt Stokes teorem, hvor integranden i flateintegralet i Greens teorem er en slags todimensjonal variant av curlen til vektorfeltet F=Pi+Qj. I to dimensjoner blir «curlen» en skalar størrelse, i motsetning til i tre dimensjoner hvor den blir en vektor. Den har en naturlig tolking som rotasjonshastighet for partikler som følger strømmen gitt ved feltet.
Greens teorem kan også tolkes som et todimensjonalt divergensteorem, om man først erstatter Q med P og P med -Q.
Deretter startet jeg på avsnitt 15.5: Flateintegraler. Grovt sett forholder disse integralene seg til dobbeltintegraler som kurveintegralene forholder seg til det vanlige enkeltintegralet. Jeg tok utgangspunkt i integralet for arealet av en parametrisert flate og definerte mer generelle flateintegraler ved å putte inn en ekstra funksjon i det integralet. Dette rettferdiggjøres best ved å betrakte Riemannsummer slik det er gjort i boka, men jeg gikk så nøye inn på det. Flateintegraler kan brukes til å beregne massen av en flate med variabel massetetthet (målt i masse per areal), og til å beregne massesenter og treghetsmomenter med formler helt analoge til de dere kjenner fra kurveintegraler og trippelintegraler. Den andre viktige anvendelsen av flateintegralene er til å beregne fluks av et vektorfelt gjennom en flate. Jeg forklarte kort hvordan definisjonen fungerer, men nådde desverre ikke noe eksempel. For å betegne fluksen er det viktig å ha klart for seg i hvilken retning gjennom flaten fluksen skal regnes som positiv: Det vil si, hvilken retning man skal velge for flatenormalen n. Flater hvor denne retningen kan velges konsistent kalles orienterbare. Et eksempel på en ikke orienterbar flate er Möbiusbåndet. Du kan lage et selv ved å ta en papirstrimmel, og lime sammen endene - ikke som en sylinder, men du snur den ene enden før du limer.
Maple-regnearket fra forelesningen er tilgjengelig.
Avsnitt 15.5 fortsatt.
Avsnitt 15.7: Stokes teorem som er et fundamentalteorem for flateintegraler.
Først en del mer om fluksen av et vektorfelt, som et flateintegral. Man får litt nyttig kansellering når man skriver ut ndS etter parametrisering, men det er viktig å passe på retningen på normalvektoren n! Hvis parametriseringen ga n i motsatt retning av det ønskede, er det bare å multiplisere med -1, så dette er ikke noe problem - bare man ikke glemmer å tenke på det. Jeg regnet eksempel 5 i 15.5 både slik som det sto i boken, og ved å parametrisere paraboloiden ved hjelp av polarkoordinater helt fra utgangspunktet. Det siste ble litt mer arbeid, men vi kan håpe det var instruktivt.
Så startet jeg på avsnitt 15.7, om George Gabriel Stokes teorem (husk at den siste s-en er en del av navnet hans). Beviset bruker Greens teorem, og forklarer kanskje hvorfor vi kan kalle Stokes teorem «Greens teorem på krumme flater». Jeg har en kort-kort (sylkort!) versjon av beviset tilgjengelig, som Postscript (skjermvennlig, utskriftvennlig) eller PDF (skjermvennlig, utskriftvennlig). Side tre i mininotatet er det jeg viste ganske kjapt på overhead mot slutten av timen (den siden er ikke videre instruktiv, men er bare en stor og stygg utregning av en viss identitet).
Først i stor detalj om sammenhengen mellom retningen på normalvektoren n omløpsretningen på randkurven C i Stokes teorem: Jeg forklarte hvordan denne sammenhengen følger fra beviset for Stokes teorem jeg ga tirsdag. Jeg liker best denne formuleringen: Ta en spasertur langs randkurven i positiv retning, og slik at hodet ditt peker i samme retning som normalvektorene i nærheten. Da har du flaten på venstre hånd. (På høyre hånd har du avgrunnen. Går du for langt til høyre, faller du ned og slår deg ihjel. Hvis du ikke gjør dette i Australia, da. Da faller du sikkert opp i stedet?)
En alternativ formulering er at du skal rundt randkurven mot klokka dersom du ser flaten slik at normalvektoren peker mot deg. Problemet med den siste formuleringen er at den bare er pålitelig når flaten er noenlunde flat: Betrakt for eksempel et kuleskall hvor du har skåret bort et lite sirkulært område. Hvis S er det som er igjen av kuleskallet, så har den normalvektorer i nesten alle mulige retninger, og det er veldig fort gjort å bli forvirret.
Jeg regnet oppgave 15.7.9, og avsluttet med å snakke om tolkningen av curlen til et vektorfelt, ved å konsentrere meg om lineære vektorfelt: De kan beskrives ved en matrise, og curlen til vektorfeltet avhenger bare av den antisymmetriske delen av matrisen. Ser man så på et vektorfelt med en rent antisymmetrisk matrise, så er det gitt ved kryssprodukt med en konstant vektor, og svarer til hastighetsfeltet i et stivt legeme som roterer med vinkelhastighet lik denne vektoren. Curlen blir to ganger vinkelhastigheten.
Harald Hanche-Olsen 2001-04-13 17:04:24 UTC