SIF5005 Matematikk 2 for F1 2003


Dette semesteret vil jeg forsøke å la denne siden gå i en tilnærmet blog-stil, altså alltid med det ferskeste materialet på toppen. (Men generelle kommentarer for en gitt uke vil likevel stå over dagene i den uken, og eventuelle planer for ukene fremover vil stå aller først.) Det betyr at du må starte på bunnen og lese deg oppover om du vil ha sammenhengen, men det er mer praktisk på denne måten om du bare er interessert i det nyeste.
Brukt til repetisjon og oppsummering.
Siste forelesning. Jeg brukte en halvtime på «teoridelen» av oversikten (se torsdagens omtale), og gikk gjennom oppgave 8, 7, 6 og 3 fra eksamen i mai 2002.
Jeg har oppsummert i det vide og det brede. Jeg tok for meg «håndtverksdelen» av kurset. Spesielt ga jeg (kjapt) definisjonen av smygsirkelen, som jeg nok hadde glemt da vi hadde om krumning og akselerasjon. Se avsnitt 12.6, nederst side 760.
Jeg har satt opp en punktvis liste ved hjelp av Maple, som jeg hadde tenkt å ha på lerretet over tavla. For sent kom jeg på at dagens forelesning er i S6, ikke R2. Nåvel, her er listen likevel, som pdf (greiest) eller mws (Maple-regneark, men nesten uten matematikk og helt uten bilder).
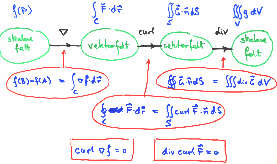
Jeg startet med å repetere litt om divergensteoremet, og brukte det til å vise hvordan man kan bruke det (sammen med noen symmetribetraktninger) til å beregne tyngdefeltet inne i jorden. Deretter tok jeg for meg hele sekvensen fra skalare felt via gradienten til vektorfelt og videre via curl til nye vektorfelt, og endelig via divergensen til skalare felt. Går du to trinn mot høyre i diagrammet ender du med null, og det har sammenheng med at randen til et legeme er en lukket flate, eller at randen til en flate er en lukket kurve. Det har også sammenheng med likheten av blandede partiellderiverte. Det at curlen til en gradient er null kan faktisk brukes til å vise denne satsen.
Transparenten jeg brukte finnes på bildet, som selv er en lenke til en større utgave (klikk på bildet og se). Et skalart felt er for øvrig ikke annet enn en funksjon.
Da fikk jeg samtidig anledning til å si det jeg nok hadde glemt tidligere, nemlig at et vektorfelt er konservativt hvis og bare hvis det er rotasjonsfritt (altså har curl null), så lenge vi arbeider i et enkeltsammenhengende område.
På samme måte er det slik at et vektorfelt som er divergensfritt (har divergens null) selv kan skrives som curl til et annet vektorfelt, igjen under visse forutsetninger om området. Men dette havner utenfor pensum. Jeg har skrevet et lite notat om det for de som måtte ha interesse (pdf, ps).
Til slutt regnet jeg en eksamensoppgave, nemlig nummer 7 fra mai 2001. Og så begynte jeg så vidt på nummer 8, men det ble ikke tid. ...
Noen avsluttende ord om Stokes' teorem, deretter avsnitt 15.6, om divergensteoremet (også kjent som Carl Friedrich Gauss' teorem).
Jeg brukte et Mapleregneark til å visualisere noen flater og legemer.
Avsnitt 15.5 og 15.7. (Merk: vi tar 15.6 til slutt, fordi Stokes' teorem erfaringsmessig faller vanskeligere i praksis enn divergensteoremet.) Det har handlet om flateintegral, og deretter George Gabriel Stokes' teorem, som viser at curlen til et vektorfelt virkelig har med rotasjon å gjøre. (Legg merke til s'en til sist i navnet til Stokes: Det heter ikke «Stoke's teorem»!)
Underveis fikk vi vite at den første vinneren av Abelprisen ble Jean-Pierre Serre.
For øvrig handlet det om avsnitt 15.7, altså Stokes' teorem. Jeg skrev opp teoremet og forklarte hvordan man skal orientere randkurven: Når du spaserer langs randkurven rundt «normalskogen» (skogen av normalvektorer til flaten) skal du ha denne på venstre hånd (hvor retningen på normalen bestemmer hva som er «opp» - trær vokser som kjent oppover). Jeg demonstrerte at Stokes' teorem er det samme som Greens teorem for et område i xy-planet. Jeg ga også et bevis for Stokes's teorem ut fra Greens teorem, anvendt i parameterområdet for flaten. Interesserte kan finne beviset som et lite tresiders notat: pdf, ps.
Til slutt sa jeg en god del om sammenhengen mellom Stokes' teorem og betingelsen for at et gitt vektorfelt skal være konservativt, nemlig at curlen er null. Denne betingelsen er alltid nødvendig, men er tilstrekkelig kun på enkeltsammenhengende områder.

Litt repetisjon, deretter avsnitt 15.5 om flateintegralet. Med utgangspunkt i integralformelen for arealet av en parametrisert flate definerte vi flateintegralet ved simpelthen å putte inn en funksjon i arealintegralet. Flateintegraler generelt deler en vanskelighet med integralet for areal, at en kvadratrot som oftest kommer i veien slik at man ikke klarer å løse integralet. For fluksintegralet, som er det vi oftest trenger, er heldigvis ikke det noe problem. Til gjengjeld må flaten være orienterbar, det vil si at den bare har én side, slik at man kan velge enhetsnormalen konsistent over hele flaten. Båndet til August Ferdinand Möbius (bildet) er et eksempel på en ikke-orienterbar flate. Jeg regnet ut noen flateintegraler og et fluksintegral blant annet for en halv torus.
Avsnitt 15.3 og 15.4.
Avsnitt 15.4 om George Greens teorem. I tillegg til å være interessant og nyttig i sin egen rett (for eksempel som prinsipp for planimeteret) kaster det også lys over spørsmålet om hvilke vektorfelt er konservative. Greens teorem har to tolkninger for vektorfelt, som en todimensjonal analog til Stokes' teorem, og som et todimensjonalt divergensteorem. Jeg skulle gjerne hatt ti minutter til om det siste, får prøve å ta det igjen i neste uke.
Avsnitt 15.3, om fundamentalteoremet for linjeintegralet, uavhengighet av vei og konservative felt. Jeg tok også en ekstra detalj i et bevis som boken tar for lett på, nemlig at dersom integralet er uavhengig av veien så er feltet konservativt. Beviset for den vanskelige delen av teorem 3 (at likhet av to partiellderiverte impliserer at feltet er konservativt) må utstå til etter Greens teorem (og selv da tar vi det ikke detaljert).
Jeg startet med en superkjapp gjennomgang av de praktiske sidene ved vektorfelter fra avsnitt 15.1. De to foilene jeg brukte er tilgjengelig her som ett ark (pdf, ps).
Det meste av tiden brukte jeg på avsnitt 15.2 om linjeintegralet. Først med hensyn på buelengde, så med hensyn på koordinatene. En kombinasjon av de sistnevnte leder til integrasjon av vektorfelt. Ett viktig eksempel fra fysikken er integrasjon av kraftfelt, som gir arbeidet kraften utfører når en partikkel følger en gitt bane.
Dagens forelesning fikk vel nesten en mer filosofisk natur enn en veldig praktisk innretning. Utgangspunktet var avsnitt 15.1, om vektorfelter. Jeg ga definisjonen og viste fram en del eksempler på lineære vektorfelt, som en slags standardmodell for hvordan lokale endringer i et vektorfelt ter seg. Jeg trakk parallellen med en del stoff fra Matematikk 3, men noe av det er dere ikke kommet til ennå (egenverdier og -vektorer). Jeg definerte divergens og curl for vektorfelter (rotasjon i 2 dimensjoner), og presenterte såvidt de tilhørende integralteoremene: Divergensteoremet, Stokes' teorem, og Greens teorem.
Jeg brukte et Mapleregneark til å visualisere vektorfelter.
Helt til sist sa jeg noen ord om avsnitt 15.2, det vil si linjeintegralet (som burde hett kurveintegralet). Mens det vanlige integralet vi kjenner fra Matematikk 1 gjerne kalles Riemann-integralet, antagelig fordi det var Georg Friedrich Bernhard Riemann som ga det endelige teoretiske fundamentet for dette integralet, er linjeintegralet egentlig basert på Stieltjes-integralet, etter sin oppfinner Thomas Jan Stieltjes. Men heldigvis for oss kan Stieltjes-integralet skrives om til et ordinært Riemann-integral, i det tilfelle da vektfunksjonen (den jeg kalte w i forelesningen) er deriverbar.
Denne uken er vi blitt ferdige med kapittel 14, og dermed med det meste av integrasjonsteknikker og -metoder. Det blir integrasjon i sylinder- og kulekoordinater, og beregning av overflateareal. (Men to integraltyper til dukker opp i kapittel 15: Linjeintegraler og flateintegraler.)
Avsnitt 14.8 om beregning av overflateareal. Jeg forklarte først hva en parametrisk flate er for noe. Deretter om hvordan flateelementet oppstår ved å se på et parallelogram utspent av de to tangentvektorene til flaten gitt ved de partiellderiverte med hensyn på parametrene: Arealet blir lengden av kryssproduktet. Så regnet jeg noen eksempler: Kuleskall, en funksjonsgraf, torusen, og endelig Whitneys paraply.
Jeg brukte et Mapleregneark. (2003-03-18: På grunn av et klippe-og-lime-uhell pekte denne linken på samme regneark som vi brukte sist. Det er nå rettet.)
Whitneys paraply er nokså interessant: Et raskt søk i google på «whitney umbrella» gir mange treff. Legg merke til at parameterfremstillingen r(u,v) er kontinuerlig og deriverbar med hensyn på parametrene. De to partiellderiverte er forskjellig fra 0 og ikke parallelle med hverandre, med bare ett unntak: (u,v)=(0,0). Så flaten her et isolert singulært punkt i origo. Denne singulariteten kan ikke fjernes ved å endre flaten litt: Den er stabil. Og det kan vises at alle stabile singulariteter av avbildninger fra planet inn i rommet er essensielt ekvivalent med denne.
Denne forelesningen ble viet avsnitt 14.7 om integrasjon i sylinder- og kulekoordinater. Vi fant volumelementene ved å kikke på små, nesten rektangulære bokser som man får ved variere hver av variablene i koordinatsystemet over et lite intervall. Det er bare en formel å huske for hvert koordinatsystem, i tillegg til definisjonen av selve koordinatsystemet selvsagt. Resten av kunsten er å finne en fornuftig rekkefølge å integrere i, og riktige grenser for integralet.
Jeg brukte et Mapleregneark nok en gang.
Det handlet mest om 14.6, det vil trippelintegraler, som er akkurat som dobbeltintegraler, bare mer: Eneste nye vanskelighet har å gjøre med at det ofte kan bli noe mer vrient å finne riktige integrasjonsgrenser.
Til sist sa jeg litt om massesenter og treghetsmoment, både i to og tre dimenjoner - dermed er vi også ferdig med 14.5.
Jeg kunne ikke helt slippe taket i polarkoordinater: Jeg var bare nødt til å bruke litt tid på berømt integral, nemlig integralet av exp(-x2) fra minus til pluss uendelig. Det tilhørende ubestemte integralet kan ikke løses ved elementære funksjoner, men likevel så vi at det bestemte integralet kan løses ved hjelp av et trick, nemlig å integrere exp(-x2-y2) både i rektangulære koordinater og i polarkoordinater.
For øvrig dekket jeg det meste av avsnitt 14.5. Det vil si, først noen flere anvendelser av dobbeltintegralet: Sentroide og massesenter for tynne plater, og teoremene til Pappus fra Alexandria.
Fremdriftsplanen sa vi skulle bli ferdige med 14.4 denne uken, og det synes jeg vi har klart.
Det ble mer om volumberegninger (avsnitt 14.3) med dobbeltintegraler, deretter dobbeltintegrasjon i polarkoordinater (avsnitt 14.4).
Jeg brukte et Mapleregneark denne gangen og.
Det handlet om dobbeltintegraler (avsnitt 14.1-2): Over rektangler, over mer generelle områder, og litt fra avsnitt 14.3 om bruken av dem til å beregne volumer.
Jeg brukte et Mapleregneark.
Vel, jeg har nettopp overlevd alle forkjølelsers bestemor (er ennå ikke helt frisk), og er nå (mandag kveld) helt i bakleksa hva planlegging angår. Men jeg holder forelesningene selv igjen, tempoplanen sier jo 13.9 og 14.1-2 men rakk bare såvidt å starte på 14.1.
Jeg ble ferdig med avsnitt 13.9, spesielt Lagranges metode med tre variable og to bibetingelser. Deretter hadde jeg bare litt tid til å starte på kapittel 14 og begynne å se litt på dobbeltintegraler: Jeg introduserte Riemannsummer for dobbeltintegralet over et rektangel, og forklarte kort hvordan dobbeltintegralet i praksis kan regnes ut med et iterert integral.
Det handlet om avsnitt 13.9, altså optimalisering med bibetingelser og Joseph-Louis Lagranges metode. Jeg forklarte geometrien og regnet et par eksempler med to variable og en bibetingelse (eller føring - disse ordene er synonyme i denne sammenhengen).
Jeg brukte et Mapleregneark.
Jeg var fortsatt syk, og Marius Irgens vikarierte. Etterpå sendte han meg en mail med omtrent dette referatet:
Totalt burde vi være ferdige med 13.8, bortsett fra kjerneregelen på vektorform.
Jeg var syk, og Marius Irgens vikarierte. Etterpå sendte han meg en mail med dette referatet:
Vi gikk gjennom 13.6, og brukte kanskje litt mye tid på det. Jeg gikk først raskt gjennom en varialbel igjen, og vektla at det vi egentlig gjorde var å bruke tangentlinjen. Da vi kom til 2 variabler snakket vi ut ifra at vi ønsket å bruke tangentplanet, så vi tok et eksempel, fant planet, og brukte det. Gikk deretter raskt over "kokebokmetoden" i boka, og sa litt kort om hvorfor dette er det samme som det vi nettopp gjorde. Det kom noen spørsmål om hva med høyere ordens Taylor, og vi lot det stå som et åpent spørsmål, men med anntydning om at i stedet for å finne det beste førstegradspolynomet så vi nå etter andregrad.
13.7: Vi fikk gjort det meste, men en kort repetisjon hadde ikke skadet dem. Igjen gikk vi raskt over envariable situasjonen og "forklarte" litt hvorfor den virker. Kopierte deretter det argumentet. Prøvde å ta begge ut i fra konkrete eksempler først, og deretter generelt. Tok noen "eksempler" med varierende anntall variabler her og der, og avsluttet med det generelle utsagnet i boken. Vi tok et konkret lett eksempel på implisit derivering (w2=x2+y2), og stoppet der. M.a.o. Vi gikk ikke gjennom utsagnet generelt, men de burde være i stand til å utføre det. Vi snakket ikke om matriserepresentasjon i det hele tatt.
Etter tempoplanen var det 13.4-13.5, 13.10 og 13.6 som sto for tur. Jeg nådde ikke 13.6, ellers er vi i rute omtrent.

Jeg gjorde meg først ferdig med avsnitt 13.5 om optimering, med teoremet om eksistens av ekstrempunkt for kontinuerlige funksjoner på et lukket og begrenset område. Jeg regnet noen eksempler for å vise hvordan teoremet brukes i praksis for å finne globale ekstrempunkt, også i på åpne, ubegrensede områder (så lenge man har god oversikt over oppførselen til funksjonen når man nærmer seg kanten eller går uendelig langt ut).
Deretter fra avsnitt 13.10 om klassifisering av kritiske punkt, med utgangspunkt i det kritiske punktet (0,0) for funksjonen (A/2)x2+Bxy+(C/2)y2. Men jeg rakk ikke si hvorfor dette eksemplet er så typisk for den generelle situasjonen: Det har å gjøre med Taylors formel i to variabler. Avsnitt 13.6 ble det ikke tid til.
Start på avsnitt 13.4 om partiellderivasjon. Jeg brukte en del tid og krefter på å motivere. Egentlig er det ingen dype hemmeligheter i det å partiellderivere: Det er akkurat som vanlig derivasjon, bare man passer på å regne de variablene man ikke deriverer med hensyn på som konstante. Vi lærte også å finne formelen for tangentplanet til grafen. Jeg nevnte at det ikke er nok at de partiellderiverte skal eksistere for at tangentplanet skal kunne sies å eksistere, de må også være kontinuerlige i en omegn. (Se for øvrig teorem 1 side 839 i E&P; avsnitt 13.6.) Som en del av motivasjonen var jeg så vidt inne på lineær tilnærming og differensialet slik det er definert i avsnitt 13.6. Når vi kommer dit, kommer jeg til å regne med at jeg har motivert dette, så jeg kommer til å ta det forholdsvis raskt.
Jeg introduserte også høyere ordens (i hvert fall annen ordens) partiellderiverte, fortalte litt om hva de blandede partiellderiverte betyr, og hvorfor de normalt er lik hverandre.
Jeg brukte et Maple-regneark for å illustrere. Jeg antydet også såvidt et bevis for likhet av blandede partiellderiverte. Jeg brukte en håndfull elektroniske transparenter (pdf) til beviset. (De har bare formler, og er kanskje ikke så lette å tolke uten figuren jeg tegnet på tavlen og alt det jeg sa underveis.)
Jeg kom også så vidt i gang med avsnitt 13.5 om optimering. Jeg fortalte at lokale ekstrempunkt må være kritiske punkter, og regnet et lite eksempel.
Etter tempoplanen skulle vi dekket 13.1-13.4. Jeg ble nesten ferdig med 13.3.
Startet på kapittel 13, etter først å ha avsluttet avsnitt 12.8 med noen innslag fra samme Maple-regneark som sist. Avsnitt 13.2 handler generelt om funksjoner av to variabler, deres grafer, hvordan visualisere slike funksjoner (for eksempel via nivåkurver, som høydekurvene på et kart), og noen teknikker for å drøfte en funksjonsgraf ut fra en formel (hva skjer om du lar x være konstant? eller y?).
Jeg brukte et Maple-regneark for å illustrere.
Avsnitt 13.3 er om grenser og kontinuitet. Grenser i to eller flere variable er vanskeligere enn i en, blant annet fordi vi ikke har teknikker som L'Hôpitals regel tilgjengelig. Jeg beregnet en del grenser (se slutten på Maple-regnearket over), nådde ikke si noe om kontinuitet. Men der er det ingen overraskelser: At en funksjon er kontinuerlig i et punkt betyr at den har en grense lik funksjonsverdien i punktet. Og vi har regler akkurat som i en variabel, som sier at alle slags sammensetninger av kontinuerlige funksjoner er kontinuerlig. Så kontinuitet er som regel lett å sjekke i de fleste punkter; det er lett å finne ut hvor problemer kan oppstå, men å sjekke kontinuitet i problematiske punkter kan til gjengjeld bli nokså vrient.
I dag kom jeg gjennom 12.7 og 12.8, så nå ligger vi presis en forelesningsdobbelttime «etter skjema».
12.7 om diverse flater i rommet og deres ligninger: Jeg viste en del eksempler, mest basert på et Maple-regneark.
12.8 om sylinder- og kulekoordinater: Igjen basert på resten av regnearket ovenfor. Sylinderkoordinatene består i å oversette x og y til polarkoordinater mens vi beholder z uberørt. For kulekoordinater bruker vi to vinkler for å bestemme en retning, og en koordinat for avstanden til origo.
Etter tempoplanen skulle vi alt gjøre oss ferdig med kapittel 12. I praksis nådde jeg bare 12.5 (kurver og bevegelse i rommet) og 12.6 om krumning og akselerasjon (med en aldri så liten tur innom 12.7 på slutten av torsdagen.) Siden det allerede er tirsdag i uken etter når jeg skriver dette, tror jeg ikke det har stor hensikt å gå mer i detalj nå. som jeg tror skal gå ganske greit - og etterpå 12.7, som omhandler en del flater i rommet og deres ligninger. Det er vel tvilsomt om vi rekker stort av 12.8 (sylinder- og kulekoordinater), men tiden vil vise.
Planen var å gå friskt ut med en superkjapp gjennomgang av vektorregning som gitt i E&P avsnitt 12.1-12.6 omtrent.
I praksis nådde jeg bare ut 12.4.
Tom Lindstrøm ved Universitetet i Oslo har laget et kompendium i Vektorregning, som tross undertittelen «En kort innføring for MAT 100» er 75 sider langt. Tilgjengelig som PDF eller PostScript. Det kan hende noen finner det nyttig.
Stort sett avsnitt 12.3-12.4: Kryssprodukt, trippelprodukt, determinanter (2×2 og 3×3). Regneregler. Symmetri! Deretter linjer og plan i rommet.
Det ble svært langt mellom eksemplene, det skal nok bedre seg etterhvert.
Mest avsnitt 12.1-12.2. Jeg klarte (selvsagt) ikke la være å presentere et enkelt bevis for Pythagoras' teorem. Ellers handlet det om elementær vektorregning i to og tre dimensjoner, inklusive skalarprodukt og ortogonalitet. (Jeg foretrekker ordet ortogonal fremfor synomymet perpendikulær, rett og slett fordi det er færre stavelser.)
Oppdatert: 2003-04-29 15:55