
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.
Se bildene: Forumet er godt besøkt!
Annonseringene i omvendt kronologisk rekkefølge.
Fra Sharkovskis teorem til kaos
Du kan også lese sammendraget som en PDF-fil.
Som mange antakelig allerede er kjent med, har funksjonen S(x) =µx(1-x), 0<x<=4, en del interessante egenskaper, som den deler med en stor klasse av funksjoner av liknende form. La I=[0,1]. Da vil S:I->I, og det viser seg at nesten uansett hvordan x0 velges i I, så vil følgen {xj} hvor xj=S(xj-1), j = 1, 2,..., oppføre seg på en måte som sterkt avhenger av verdien på parameteren µ. For noen verdier er oppførselen (omsider) periodisk, mens den for andre verdier vil være kaotisk. Sharkovski (1964) har vist følgende perle for det periodiske regime:
De naturlige tall kan ordnes (totalt) på en slik måte at om p er større enn q iht Sharkovskis ordning, så har S periode q dersom S har periode p.
3 er det største tallet i Sharkovskis ordning. Det betyr at hvis S har periode 3, så har S enhver periode.
Etter en lett diskusjon av Sharkovskis teorem, vil fordraget dreie over mot en diskusjon av mer statistisk orienterte metoder for å studere kaos i ikkelineære dynamiske systemer.
Pseudotall og pseudonumerikk - bedre symboler og ord for nummer
Romertall var egnet for telling.
Arabertall er bedre, egnet også for matematikk.
Ti nye symboler, som jeg døper pseudotall, er
enda bedre, egnet også for husking. Pseudotall har form
etter konsonantbokstaver med gjennomstrek
(S T
N M
R L
J K
F P > 0 1 2 3 4 5
6 7 8 9) og kan huskes som ord. F.eks. 907842
blir PSKFRN, som kan huskes som ordet
PåSKeFeRieN. I vår tid er nummerhusking spesielt
nyttig, fordi tall brukes til identifikasjon. Jeg tror
at identifikasjonsnummer, som ikke kan huskes, villeder
barn til å tro at nummer og matematikk er umulig og
uinteressant.
Våre arabertall-symboler er brukbare for skriftlig
arbeid, men våre ord for tall er helt uegnet for
mentalt arbeid. 907842 heter «ni hundre og sju tusen,
åtte hundre og førtito», altså 15 stavelser for et
6-sifret nummer. Både symboler og ord for tall bør være
korte og visuelt beslektet. I mitt nye nummersystem,
som kalles pseudonumerikk, er nummeret
PSKFRN skrevet som ordet:
«jiPiSiKiFiRiNi» (på Engelsk: «yiPiSiKiFiRiNy»).
Kanskje pseudonumeraler og pseudonumerikk vil slå an, og forhåpentligvis fortere enn arabertall gjorde i sin tid. Det tok ca.400 år før arabertall erstattet romertall i Europa.
Las Vegas, aksjer og matematikk
Det finnes en enorm mengde litteratur på både spillteori og modellering av aksjekurser. Vi skal ikke forsøke å gi noen generell oversikt, men heller velge ut en strategi, som ved visse forutsetninger er ideell. Problemet er som følger:
Du har et spill med gunstige odds, men du har begrenset med penger. Hvordan skal du få gevinsten til å gå mot uendelig fortest mulig uten risiko for å tape alle pengene?
Presentasjonen vil bli gitt på et nivå hvor alle skal kunne følge med på det som skjer, og kanskje bli fristet til å gamble litt...
Eksakt simulering ved bruk av Markovkjeder
Stokastisk simulering ved bruk av Markovkjeder, med alle dets anvendelser og implikasjoner, er kanskje det største fremskritt innen statistikken de siste ti-år. Ett av problemene som en alltid støter på, er når har Markovkjeden konvergert? Jeg skal presentere en meget elegant og enkel «løsning» på problemet, som gjør at en for noen modeller kan få eksakte sample fra Markovkjedens grensefordeling.
Alle de grunnleggende begrepene (slik som Markovkjeder, for eksempel) vil bli definert.
Kuriositeter fra Normats oppgavespalte
I tidligere foredrag i serien «Matematiske perler (og kuriositeter)» har perlene fått sin plass. Nå er det på tide at kuriositetene slipper til.
Som oppgaveredaktør i Normat har jeg kommet borti en del fakta som jeg ikke kjente fra før, og jeg vil presentere noen av de mest kuriøse (og et par litt mer seriøse). Vi skal se på en generalisering av binomialsetningen, entomologiske uhell på et polyeder, en kuriøs faktorisering av oddetall, hvilke kjegler som skjærer et plan i en gitt ellipse, og en kurve knyttet til vinkelhalvering.
Om Abels tapte manuskript, der han blant annet viser at
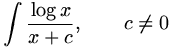
ikke er en elementær funksjon
Det første arbeidet Abel skrev på fransk -- noe som understreker den betydning han la i det -- er fra vinteren 1822/23, da han var 20 år gammel. Det omhandler («ubestemte») integraler av elementære funksjoner, og gir kriterier for når disse igjen er elementære funksjoner. Fra hans matematiske dagbok fra dette tidsrommet står det i en fotnote at han i det omtalte arbeidet blant annet har vist at
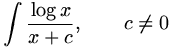
ikke er en elementær funksjon (dvs. ikke kan
uttrykkes på endelig form ved algebraiske, logaritmiske
og eksponensielle funksjoner. [Husk: de trigonometriske
funksjonene samt deres inverse arcus-funksjoner, kan
uttrykkes ved de (komplekse) eksponensial- og
logaritme-funksjonene!] Flere matematikere, blant annet
Laplace, hadde tidligere forsøkt å vise at integralet
av visse elementære funksjoner ikke er elementært, men
ingen hadde lykkes.
Manuskriptet til Abel sirkulerte blant forskjellige
kontorer ved universitetet i Christiania som bilag til
hans søknad om et reisestipend. Tilslutt forsvant det i
en eller annen byråkratisk skuff, og er gått tapt. Det
ble Liouville som 4 år etter Abels død tok opp igjen
dette aspektet ved integralregningen, og presenterte en
omfattende teori. Imidlertidig tilkjennegir Liouville
sin gjeld til Abel, idet det i Abels (senere)
forskjellige publikasjoner finnes spredte resultater
som er meget relevante for dette studiet, spesielt i
hans siste store artikkel om elliptiske funksjoner,
«Précis d'une théorie des fonctions elliptiques». I
sitt siste brev til Legendre, få måneder før sin død,
sier Abel at han er i besittelse av en omfattende teori
om integraler, men at han ikke har hatt tid til å
skrive det ned. Han nevner spesifikt teoremer som
forespeiler Liouvilles senere resultater, og som til og
med overgår disse. (I et brev til Sophus Lie fra 1882
skriver den aldrende Weierstrass at det nettopp var
brevet fra Abel til Legendre (som han fikk tilgang til
via Crelle), som i sin tid førte han selv inn på den
matematiske løpebanen, idet han løste et av de
problemene Abel der hadde stilt åpent om ubestemte
integraler.)
Vi vil forsøke å rekonstruere noen av de ingrediensene som antagelig har inngått i Abels tapte manuskript, og samtidig påpeke hvordan dette tilsynelatende noe sterile emnet har tilknytning til både ligningsteorien, og til studiet av de såkalte abelske integraler.
Vi kjenner alle polyedre som er rigide. Terninger og tetraedre for eksempel. I 1766 framsatte Euler en hypotese om at alle polyedre var rigide. (Vi tenker oss her polyedre i rommet med sider av stiv kartong, og som er fleksible langs kantene.) Unge Cauchy greide å vise Eulers hypotese for konvekse polyedre, men i 1896 viste Raoul Bricard at det finnes fleksible oktaedre, dessverre med en liten hake: Flatene går gjennom hverandre, slik at oktaedrene ikke kan lages av kartong, for eksempel.
Historien tok en uventet vending i 1970-årene, og problemet viste seg å ha flere overraskelser på lager.
Først fant Robert Connelly et fleksibelt polyeder (uten selvskjæringer) som han presenterte på den internasjonale kongressen for matematikere i Helsinki i 1978. Dennis Sullivan laget et nøyaktig fleksibelt polyeder med et bittelite hull og fylte det med røyk. Etterpå kunne Sullivan observere at det ikke ga fra seg noe røyk uansett hvilken vei polyederet gjennomgikk fleksen. Dermed hadde Connelly og Sullivan god grunn til å fremsette «belgformodningen,» som ble til et teorem i 1997.
Beviset for dette teoremet foregår ved en ganske finurlig induksjon, som lett lar seg presentere på tavlen for en generell forsamling av vanlige matematikkstudenter. Det bemerkelsesverdige er at det teknisk vanskelige trinnet i beviset (som vi så vidt vil berøre) bygger på en teori som har vist seg senere å være like viktig i tallteori som i geometri. Denne teknikken er også av avgjørende betydning for så vel Gerd Faltings bevis for formodningene til Mordell, Tate og Shafarevich, som i Andrew Wiles bevis for Taniyama-Shimuraformodningen i det stabile tilfellet, som jo ifølge Kenneth Ribet og Barry Mazur medfører det berømte Fermats siste «teorem.»
«Alle» kjenner vel Peanokurven: En kurve som helt fyller et kvadrat i planet. En kurve i denne sammenhengen er en kontinuerlig funksjon fra intervallet [0,1] inn i planet. Det er klart at en kurve med Peanokurvens egenskaper ikke kan være en-til-en; tvert i mot må den skjære seg selv uendelig ofte.
En skulle tro at en kurve som aldri skjærer seg selv (og altså etablerer en homeomorfi mellom [0,1] og sitt bilde i planet) må være ganske tynn. Det vakte derfor berettiget oppsikt da Osgood fant en enkel kurve i planet med positivt areal for snart 100 år siden.
Konstruksjonen av Osgood-kurven er ikke mye vanskeligere å forstå enn den for Peanokurven. Jeg vil starte fra begynnelsen, med en kort omtale av Peanos opprinnelige definisjon. Så vil jeg presentere Hilberts betydelig forenklede konstruksjon, og til slutt vise hvordan en variant av denne resulterer i Osgood-kurven.
Vi vil omtale to problemer som går tilbake til Pompeiu og Steinhaus, henholdsvis. Disse problemene har tilsynelatende ingenting å gjøre med hverandre, men begge omhandler Euklidske bevegelser (translasjon + rotasjon) i planet. Deres elementære formulering er besnærende.
«Kan alle plasseringer av en plan mengde inneholde nøyaktig et gitterpunkt?» Dette er Steinhaus' problem. Alle indisier tyder på at problemet har et negativt svar, men noe bevis foreligger ikke.
Pompeiu-problemet dreier seg om integraler av (kontinuerlige) funksjoner som forsvinner. Det har en overraskende forbindelse med et overbestemt randverdi-problem (Shiffers problem), som kan spores helt tilbake til Lord Rayleighs bok «The Theory of Sound.»
S. Jackson & D. Mauldin har konstruert en mengde i planet med den såkalte Steinhaus-egenskapen. Denne mengden er ikke Lebesgue-målbar! (Journal of the AMS 15 #4, 817–856.)
I 1899 oppdaget Frank Morley et av de mest overraskende, og totalt uventede, teoremene innen elementær Euklidsk geometri--et teorem som bedømt utifra et rent estetisk synspunkt har få rivaler: Tredel hver av vinklene i en vilkårlig trekant og finn tre skjæringspunkter. Disse er hjørner i en liten trekant inne i den opprinnelige. Den lille trekanten er likesidet(sic!).
Selv om det finnes mange forskjellige bevis for Morleys teorem, så gir ingen av disse noen forklaring på hvorfor et slikt resultat er mulig, og hvorfor det ikke kan generaliseres. Alain Connes (Fields-medaljevinner i 1982 og Crafoord-prisvinner i år) har nylig gitt et nytt bevis for Morleys teorem som for første gang gir en begrepsmessig forståelse og forklaring av det som er blitt kalt "Morley-miraklet".