
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.
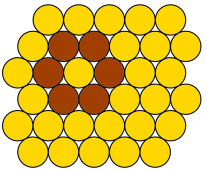
Vi har alle lekt med mynter og prøvd å «pakke» dem sammen. Hvis myntene er like store, kan hver mynt omkranses av 6 andre. Dette er et enkelt eksempel på en sirkelpakking. Generelt er en sirkelpakking en konfigurasjon av sirkler som tilfredsstiller gitte berøringsmønstre.
Med sirkelpakking mener vi ikke det vi kan kalle to-dimensjonal kulepakking, som handler om å pakke jevnstore sirkelskiver mest mulig effektivt i planet. Axel Thue viste i 1890 at den «åpenbare» løsningen (bildet) er optimal. I en generell sirkelpakking tillater vi sirkler av forskjellige størrelser.
Til tross for at sirkelen har vært studert i tusenvis av år er idéen om sirkelpakkinger relativt ny. I 1985 holdt William Thurston et foredrag med tittelen A finite Riemann mapping theorem, hvor han introduserte sirkelpakkinger. Senere har særlig Kenneth Stephenson gjort en innsats for å gjøre sirkelpakkinger mer kjente.
I dette perleseminaret vil vi se litt nærmere på hva sirkelpakkinger er, og hvordan de kan konstrueres. Rigiditeten i sirkelpakkingene har mye til felles med rigiditeten i konforme avbildninger. Vi vil bruke dette til å formulere diskrete versjoner av flere klassiske resultater innen kompleks analyse.

Lennart Carleson er vinner av Abelprisen for 2006. Han beskrives som en nyskapende problemløser: Han har løst sentrale og vanskelige problemer og samtidig skapt teknikker som har hatt stor innflytelse på utviklingen av moderne analyse.
Følgende treffende karakteristikk av Carlesons arbeid er gitt av Peter Jones:
The problems he considers are always extremely concrete and
the statements of his theorems are easily understood by any
mathematician. But it is in his proofs where one sees the
unmistakable stamp of Carleson. In virtually every major work
there is an involved geometric construction carrying deep
combinatorial structure of renormalizable (scale invariant)
type.
Kan vi klare å få frem hva dette dreier seg om i et perleseminar? Vi skal gjøre et forsøk.
Seminaret vil dreie seg om selve kjernen i den såkalte koronakonstruksjonen. Problemet er hvordan vi kan kontrollere lengden til «nivåkurvene» til |f(z)| når f er en begrenset analytisk funksjon. Anførselstegnene signaliserer at vanlige nivåkurver ikke duger, men det kan vi altså gjøre noe med.
I 1770 viste Lagrange at ethvert helt tall n større eller lik 0 kan skrives som en sum av fire kvadrater, dvs. n = x2 + y2 + z2 + u2 der x, y, z og u også er hele tall. Vi kaller da den kvadratiske formen x2 + y2 + z2 + u2 universell. Formene x2 + y2 og x2 + y2 + z2 er ikke universelle. Hvilke tall representerer de? Spørsmålet om hvilke tall en gitt kvadratisk form representerer har opptatt matematikere som Diofantos, Fermat, Euler, Lagrange, Legendre, Gauss og Ramanujan.
Vi skal også se på nyere resultater fra 1993 og 2005 om hvordan en meget lett kan avgjøre om en kvadratisk form er universell eller ikke.
Geometri appellerer til fantasien og kombinerer på en god måde det umiddelbart forståelige med det mere overraskende og dybtliggende i matematikken. I dette fordrag præsenteres tre temaer fra geometrien, som jeg finder særligt fascinerende i den henseende. De tre temaer spænder lige fra geometriske problemstillinger betragtet af de gamle grækere til geometri (topologi) udviklet i det 20. århundrede. I det første tema ser vi på figurer med størst muligt areal under fastholdt omkreds (Det isoperimetriske problem). I det andet tema regner vi med fletninger, næsten som det var tal. Det tredie tema ligner for mange en tryllekunst, men der snydes ikke, når en dobbetsnoning på et par snore fjernes uden saks (Dirac's strengproblem).
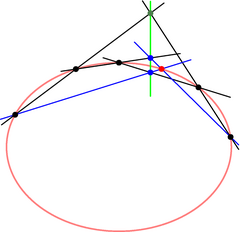
Alle vet at tre punkter i planet bestemmer en sirkel, og hvordan man konstruerer denne sirkelen. De fleste vet også at fire punkter er nok til å bestemme en parabel, og at et generelt kjeglesnitt er bestemt av fem punkter. Hvis tre eller flere av dem ligger på en rett linje degenereres kjeglesnittet til en eller to rette linjer. Det er kanskje ikke så velkjent at det finnes en metode til geometrisk konstruksjon av et kjeglesnitt gjennom fem vilkårlige punkter. Metoden går tilbake til to skotske matematikere, Braikenridge og Maclaurin (han med rekken) fra ca. 1730. Konstruksjonen representerer en omvending av Pascals berømte teorem som han fant som 16-åring: Hvis de seks hjørnene i en sekskant ligger på et kjeglesnitt, så vil de tre skjæringspunktene mellom forlengelsene av sekskantens parvis motsatte sider ligge på en rett linje.
Det er to svakheter ved Braikenridge–Maclaurins konstruksjon. Den sier ingen ting om hva slags kjeglesnitt man får, om det er en ellipse eller en hyperbel. Og prøver man å redusere antall gitte punkter til fire, i håp om få en parabel, så bryter metoden sammen.
Med dette som bakgrunn stiller vi følgende enkle spørsmål: Gitt fem punkter i planet hvor ikke mer enn to av dem ligger på en rett linje, er det mulig å avgjøre konstruktivt om de bestemmer en ellipse, en parabel eller en hyperbel? Konstruktivt betyr her ved hjelp av passer og linjal, ved standard metoder og de gitte punkter som start-data. Siden parabelen representerer en overgang mellom de to andre typene skal vi forenkle diskusjonen ved å spørre om når fem punkter vil produsere en ellipse. Det er en opplagt nødvendig betingelse: De fem punktene må danne en konveks polygon. Det er imidlertid nesten like opplagt at denne betingelsen ikke er tilstrekkelig, tenk for eksempel på fem punkter som ligger på en gren av en hyperbel.
Vi skal forfølge dette problemet, noe som leder til Den store parabeljakten (fritt etter Roald Dahl), muligens med noen små perler på veien (ingen rosiner). Som veiviser har vi CABRI, et dynamisk geometrisk program.
I 1671 oppdaget den skotske matematikeren James Gregory Taylorrekken til arctangens-funksjonen, og spesielt fant han rekken
(*) arctan 1=π/4=1−(1/3)+(1/5)−(1/7)+(1/9)−(1/11)+…
(Denne rekken ble oppdaget uavhengig av Leibniz i 1673.)
Rekken (*) konvergerer meget langsomt: Summen av de 500000 første leddene i (*) bestemmer kun de fem første desimalene i utviklingen av π. I 1706 fant den engelske matematikeren John Machin arctangens-formelen
π/4=arctan 1=4 arctan(1/5)−arctan(1/239)
og han benyttet denne til å bestemme π til 100 desimaler. Senere ble det funnet mange lignende arctangens-formler, blant annet av Euler og Gauss. I 1894 publiserte den norske matematikeren Carl Størmer den fullstendige teorien for arctangens-formler til bestemmelse av π, ved å benytte seg av teorien for de Gaussiske hele tallene Z+Zi. Størmer fant spesielt formelenπ/4=arctan 1 = 6 arctan(1/8)+2arctan(1/57)+arctan(1/239)
I 1949 brukte ENIAC, den første store elektroniske regnemaskinen, 70 timer på å beregne π til 2037 desimaler basert på Machins formel.
I 1961 brukte en IBM 7090 i underkant av 9 timer til å beregne π til 100,265 desimaler basert på Størmers formel. Fram til 1981 ble dette utvidet enormt ved kraftigere datamaskiner, hele tiden ved benyttelse av diverse arctangens-formler. Etter 1981 har man benyttet raskt konvergente rekker for π som ble funnet av den store indiske matematikeren Ramanujan tidligere i det 20de århundre. Per idag er rekorden for bestemmelse av π 1.241.100.000.000 desimaler (600 timers bruk av en Hitachi SR8000 superdatamaskin). En kuriositet: I desimalutviklingen forekommer siffersekvensen 0123456789 etter de første 1.387.594.880 sifrene bak desimalkommaet i π.
Vi skal i dette foredraget hovedsakelig konsentrere oss om Størmers studie av arctangens-formlene, og deres relasjoner til de Gaussiske heltallene.
Hele dette området kan kanskje best oppsummeres med en omskrivning av hva avdøde pave Johannes Paul II uttalte om fotball: Av alle uviktige ting innen matematikken, er dette en av de mest fascinerende.

I vår nye digitale hverdag ønsker mange av oss ofte av forskjellige grunner å dele våre hemmeligheter med fremmede, men ikke med hvem som helst. Dette gjelder f. eks. kredittkortnummer og personopplysninger.
Vi ønsker også å overbevise andre, f. eks. banken vår, om at vi er den vi er, selv om vi befinner oss på helt andre plasser i verden. Men samtidig ønsker vi at ikke andre skal utgi seg for oss. Vi skal se hvordan klassiske resultater fra tallteorien kan hjelpe oss med både dette, og noen andre mer eller mindre praktiske problemer, som å kaste krone og mynt over telefonen.
Skal vi stole på at dette virker, trenger vi å være sterke i troen på at man med gitt datakraft kan lage seg problemer som beregningsmessig er så vanskelige at man med den samme datakraft ikke kan løse det inverse problemet.
Et eksempel: På datamaskinen din kan du, med riktig programvare, finne to primtall p og q med ca. 200 siffer hver. Du kan også gange de sammen, altså finne n=pq. Men, sletter du p og q, er de tapt. Datamaskinen din vil ikke klare å faktorisere n – tror vi.
I tillegg til et lite gjensyn med Fermat og Euler, blir det kanskje tid til å se på noen mer sofistikerte måter å skaffe seg beregningsmessig vanskelige problemer på, basert på ideer fra geometri eller kombinatorisk gruppeteori.
Genren problemløsning innen matematikk er i sterk vekst over hele verden. Spennvidden er stor: Fra Sudoku-oppgaver, som avisene er fulle av, til seriøse matematikk-konkurranser som hvert år arrangeres, og der unge vordende matematikkspirer utviser imponerende kløkt og skarpsindighet. Hver sommer kulminerer dette med den internasjonale matematikk-olympiaden, IMO, som snart vil ha over 100 deltakerland. (I Mexico i år deltok over 90 land, og antallet har økt jevnt og trutt i de senere år.)
I løpet av dette foredraget vil jeg gi eksempler på løsninger av matematiske problemer hentet både fra IMO og fra andre konkurranser. (Se vedlegg.) Kriteriet for mitt utvalg har vært den «gode» følelsen som oppgaven/løsningen har gitt meg. Jeg nøler ikke med å karakterisere noen av disse eksemplene som «matematiske perler». Som leder for det norske laget til IMO ti ganger i løpet av de siste tyve årene, har jeg nok skjelet ekstra til noen av de mange gode oppgavene som er blitt foreslått som IMO-oppgaver. Jeg gir her til beste tre eksempler (lett–middels–vanskelig) på slike oppgaver, der løsningene vil bli presentert i løpet av mitt foredrag.