
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.

Vi tar utgangspunkt i problemet å løse systemet x2+u2=1 og x3u−2u3+xu−x+u=0 med to polynomlikninger i to ukjente. En smertefri løsning fremkommer ved å parametrisere enhetssirkelen, hvilket leder til spørsmålet om alle algebraiske kurver kan parametriseres globalt med analytiske funksjoner? Vi beskriver et sentralt resultat i kompleks analyse, kjent som Uniformiseringssatsen, som leder til et svar på dette spørsmålet. Satsen vil bli konkretisert ved eksempler.
To map the sphere on the plane isometrically (i.e. with a constant scaling) is impossible. Every map projection has a defect. Desirable properties such as conformality (preserving angles), area preserving, and “geodetic” (great circles being mapped on straight lines) can always be attained singly, but never together. In the lecture we will present a great number of map projections and analyze them mathematically. We will also consider different measures on the defects of projections. Finally we will consider projections of other manifolds than the sphere, e.g. the hyperbolic space.
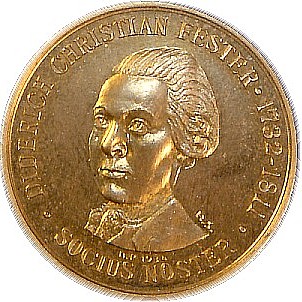
 Kranskekaken Et
overflødighetshorn – etter oppskrift fra Trondhjem
på 1760-tallet. (Klikk på bildet for større utgave.)
Kranskekaken Et
overflødighetshorn – etter oppskrift fra Trondhjem
på 1760-tallet. (Klikk på bildet for større utgave.)
Vi får møte dansken Diderich Christian Fester som kom til Trondheim i 1768 for å undervise ved Katedralskolen. Han ble også umiddelbart medlem av Det Kongelige Norske Videnskabers Selskab. Fester var selvlært, Norges første yrkesmatematiker og hadde en ukuelig tro på vitenskapens fortreffelighet. Hans historie gir et interessant tidsbilde fra vitenskapsmiljøet i Trondheim på slutten av 1700-tallet.
Magne B. Rabben vil presentere D.C. Festers historie.
Kari Hag vil kommentere et par av hans matematiske arbeider.
How to make a pearl:
If you are an oyster, this involves grit and mucus (generally agreed upon as being a bit disgusting by all except small children) and the result is a pearl. For a mathematician, irritating things include: being told something can't be done, being told that two things are similar but for there to be no connection between the two, and being told that something is true but with no reason behind it. Category theory grew out of getting rid of these irritations by covering them with structures and axioms (which most find faintly displeasing but a few find fascinating). But, over time, it has produced its fair share of gems.

(A more detailed abstract, albeit without the hyperlinks, is available in pdf format.)
At the 1987 International Mathematical Olympiad for high-school students (which was held in Cuba), one of the problems was:
“If the polynomial fp(x)=x2+x+p yields prime numbers for x=0,1,2,…,[√(p/3)], then it yields prime numbers for x=0,1,2,…,p−2.” [Note that this is optimal since fp(p−1)=p2, and so is not a prime number.]
The students were most likely not aware of the fact that the prime producing property of f_p(x) is intimately connected to a famous problem raised by Gauss in his classic book on number theory, Disquisitiones Arithmeticae, from 1801. The problem became known as the class number one problem, and more than 150 years elapsed before it was finally solved.
The Riemann hypothesis (dating from November 3, 1859, almost exactly 150 years ago to the day!) is arguably the most famous open problem in mathematics. Starting with the function ζ(s), and the Euler product formula, one can extend ζ(s) to an analytic function in the whole complex plane (except at s=1, where it has a simple pole). The location of the zeros of the zeta function ζ(s) yields highly interesting information about the distribution of the prime numbers. The Riemann hypothesis says simply that all the (non-trivial) zeros of ζ(s) lie on the so-called critical line Re(s)=1/2. Very surprisingly the Riemann hypothesis turns out to be equivalent to a seemingly completely elementary question: How do the Farey fractions differ from regularly spaced points in the interval [0,1]? The Riemann hypothesis is equivalent to a specific behaviour as n tends to infinity of how the Farey sequence of order n deviates from n uniformly distributed points in [0,1]. (This will be made precise in the talk.)
Our aim is to give an explanation or, at least, an indication, why the elementary mathematics described above are connected with deep mathematical results associated with Gauss and Riemann, respectively.
Finally – as a unifying feature in this context – we will mention an intriguing connection that exists between the generalized Riemann hypothesis and the general class number problem of Gauss.
Until the middle of the 19th century mathematics, and in particular geometry, was considered an abstract study of physical reality. In the talk I shall show how the discovery (or invention) of non-Euclidean geometry changed this view and made mathematics an autonomous science whose subject is axiomatically defined structures. This change has often been characterized as one of the few revolutions in the history of mathematics. At the same time the new geometries opened for a revolutionary change in our conception of space.
The historical talk will involve the work of important thinkers such as Euclid, Kant, Gauss, Lobachevsky, Beltrami, Helmholtz, Riemann, Clifford, Poincaré, Hilbert, Einstein and Gödel.
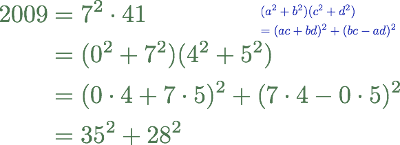
The integers like 10=12+32 that are sums of two squares have been studied for nearly four centuries, yet there are questions about them that are still open today. Among the many mathematicians who contributed to this topic were Fermat and Gauss. Indeed some reckon Fermat's Christmas Theorem to be the first deep result in number theory: Any prime p whose remainder on division by 4 is 1 has a decomposition p=k2+m2 as a sum of two integer squares. Even today, no proof is known that does not rely either on a highly ingenious argument or else some powerful theory.
The topic of sums of two squares is among the most classical in number theory, so the talk will emphasise historical development. The main facts known about sums of two squares will be outlined, generally without proofs. Some open questions will also discussed, though there is good reason to believe these to be quite difficult.

A Möbius transformation f(z)=(az+b)/(cz+d) – with complex coefficients a,b,c,d – is an invertible conformal map from the extended complex plane into itself. Among them, we find translations, dilations, rotations as well as inversions (with respect to circles); moreover, every Möbius transformation can be composed from a number of such maps. Using the stereographic projection from the Riemann sphere to the extended complex plane, one may think of Möbius transformations as conformal (or biholomorphic) maps from the sphere into itself. It is worthwhile to investigate their geometric, algebraic and analytic properties; in our days, many of them can be visualized by various applets on the internet.
In the late 19th century, Möbius transformations played an important role in the work of Felix Klein and Henri Poincaré in making the hyperbolic plane and hyperbolic space – until then quite abstract inventions – more easily understandable through concrete models. Certain subgroups of the group of Möbius transformations can be interpreted as isometry groups for these models. Furthermore, discrete subgroups of these isometry groups can be used to tessellate the entire hyperbolic plane by hyperbolic polygons. Several of M.C. Escher’s most fascinating pictures make use of this technique.
Imagine a bunch of circles that are paired by certain Möbius transformations: inside out, outside in! Already back in the late 19th century, Klein, Robert Fricke and Friedrich Schottky tried to find out what happens when you iterate these maps. It is amazing how close their “fractal” hand drawings come to our days computer generated pictures, that you can draw on your screen using programs on the internet. With a little experience, you can even generate very attractive pearl(!) necklaces yourself.
This talk is inspired by the beautiful book Indra’s Pearls by Mumford, Series and Wright.