Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.
Friezes are patterns of integers introduced by Conway and Coxeter in the 1970s. They are simply defined as square grids with integers on their intersection points, such that every 2×2 subgrid is a matrix with determinant one. From this simple definition arise surprising properties of integrality and periodicity. Fomin and Zelevinsky's theory of cluster algebras provides profound explanations for these various phenomena, in a vastly more general setting.
This talk will be an overview of some of these phenomena, illustrated with friezes and quiver mutation.
En cellulær automat består vanligvis av celler i et gitter, hvor hver celle kan være i en av endelige mange tilstander. Et sett med regler forteller hvordan tilstanden til hver celle avhenger av cellene rundt. Slike cellulære automater ble opprinnelig studert av Stanislaw Ulam og John von Neumann på 40- og 50-tallet, men senere utviklet til en rik teori. Vi ser på Stephen Wolframs 1-dimensjonale cellulære automater, John Conways 2-dimensjonale cellulære automater (Game of Life) og Christopher Langtons varianter av «kunstig liv» (Langton's Ant).
Det vil være anledning til å se 15 km langrenn på storskjerm i forkant av foredraget.
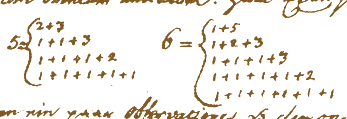Utsnitt fra brev fra Goldbach til Euler.Det har skjedd mye innenfor tallteori det siste året, særlig i forbindelse med to av de virkelig store formodningene: ABC-formodningen og Goldbachs formodning. I dette perleforedraget skal vi se litt nærmere på historien bak disse formodningene, samt hva status er i dag.
It was quite a sensation when Ben Green and Terence Tao announced in 2004 that they had proved a famous conjecture by Paul Erdős: there exist arbitrarily long arithmetic progressions of prime numbers. When Tao received the Fields Medal in 2006, this result was particularly emphasized in the citation. The Green/Tao proof rests on two sources:
Furstenberg gave a new proof of the Szemerédi result using ergodic theory, and his proof technique turned out to be very important for the Green/Tao proof. Furstenberg’s “multiple recurrence theorem”, which turns out to be “equivalent” to Szemerédi’s theorem, harks back to Poincaré and his study of the n-body problem. In fact, Poincaré’s revolutionary new point of view gave a qualitative answer to the outstanding problem of deciding whether our planetary system is stable or not – the famous Poincaré recurrence theorem from 1890 providing the answer. (Incidentally, the Poincaré result caused a controversy (“Wiederkehreinwand”) involving Boltzmann, Zermelo and Nietszche (the philosopher!).)
We will give a non-technical description of the developments that led to the proof by Green and Tao. In particular, we will show how the sieve discovered by Atle Selberg dovetails with the properties they need of the so-called “pseudoprimes” in order to accomplish the proof.
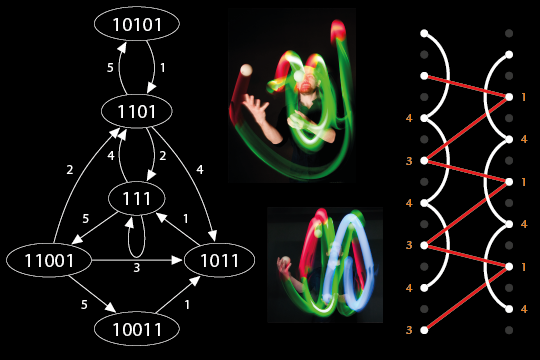
What are the connections between juggling and mathematics? In the middle of the 1980s, a mathematical analysis of juggling emerged. A notation system called siteswap was invented/discovered which enabled jugglers and mathematicians alike to define, analyze and categorize juggling patterns according to different types of throws. It turned out that there was a complex and rich world of mathematics related to juggling. In this talk, we will have a look at notation systems for juggling, Shannon's Juggling Theorem, some combinatorics, and algorithms for finding juggling patterns. Finally, there will be a demonstration of juggling balls with computers inside of them that analyzes and shows jugglings patterns in real time.
See also The Mathematics of Juggling by Burkard Polster.
Felix Klein (1849–1925) and Sophus Lie (1842–1899) met in Berlin in 1869 where they soon became close friends and collaborators. Their work from this time dealt with complex geometrical structures in 3-space, but what is remembered today are ideas that flowed from Klein’s “Erlangen Program” and Lie’s theory of continuous transformation groups, both landmarks in the history of mathematics. After 1872, however, their mathematical interests diverged. This lecture will describe the difficult partnership of Klein and Lie in the light of European mathematical relations, which often reflected national allegiances and international competition.
_-_The_Girl_With_The_Pearl_Earring_(1665).jpg){kind=link}
