
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.
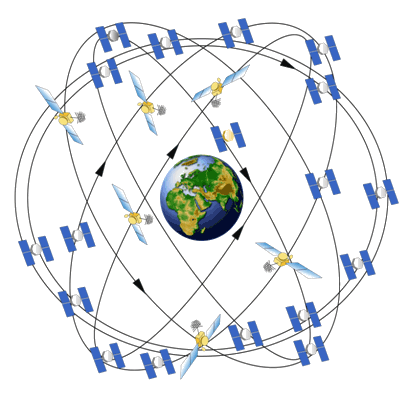
The Global Positioning System (GPS) is based on about thirty satellites in orbit around the earth, all broadcasting precise orbital and time data. GPS receivers – from handheld units to backpacks used by surveyors – use the timing of received data to determine their position. There is quite a lot of mathematics underlying the successful operation of the GPS infrastructure, and I will try to give an overview of some of it. But perhaps the most surprising aspect is the fact that relativity – both special and general – provides corrections without which the whole system would be useless. I shall try to explain the required portions of the theory, including a brief look at black holes. If we escape being swallowed by the event horizon, we return at last to relativity’s impact on GPS.
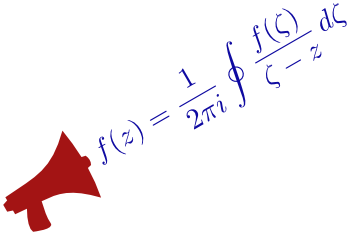
Å kommunisere matematikk avhenger av to like viktige komponenter: Kommunikasjon og matematikk. I utviklingen av matematikk-infotainment-TV-serien «Siffer», en formidabel seersuksess på NRK1 høsten 2011, koblet man en matematiker med en musikkvideo-regissør. Selv om matematikk ofte foregår inne i hodet til matematikere, er det ikke inne i hodet sitt folk flest lever; de lever av å se. «Seeing is believing». For å kommunisere matematikk må man gi folk noe å se på. Hva dette «noe» er kan være en formidabel utfordring. En utfordring som likefullt må tas på alvor dersom man skal snu den uheldige samfunnstrenden der unge i stadig økende grad velger bort matematikk.
In 2011 it was 95 years since Ludwig Bieberbach published the paper where he proved that for an analytic function of the form \(f(z)=z+\sum_{n=2}^\infty a_nz^n\), mapping the unit disk one-to-one to a region in the complex plane, the inequality \(|a_2|\le2\) holds. In a footnote he cautiously suggested that perhaps it is true in general that \(|a_n|\le n\). This was later to be known as the Bieberbach conjecture. The conjecture generated a lot of interest for almost 70 years and many attempts were made to solve it. The story ends in 1985 when Louis de Branges published his paper A proof of the Bieberbach conjecture (MR0772434) in Acta Mathematica.
In this talk I will start by discussing the situation in complex function theory in the beginning of the 20th century: What were the “hot topics” at the time, and what led Bieberbach to the work that he published in 1916? Then I will briefly discuss the various tracks that were followed over the years in order to get a grip on the conjecture. Finally, I will go into the circumstances around the proof. The proof relies heavily on the so-called Loewner theory, which has been fundamental for much of the work on the Bieberbach conjecture since the early 1920s. The proof also rests on a certain inequality for special functions, which does not appear to have anything to do with complex function theory. In particular the role of this inequality caused serious doubts about the correctness of the proof in many outstanding mathematicians when the details of the proof first became known.

At the National University of Singapore I have taught a General Education Module called “Heavenly Mathematics & Cultural Astronomy”. In this talk I will give some samples from the course. Most astronomy books are written from a “high-northern-latitude-centric” point of view. I will instead discuss the motion of the Sun and the Moon from a “hemispherically-correct” point of view.
Some of the questions we will address are: Why do clocks go clockwise? In the Bible, the prophet Isaiah made the shadow of the sundial go backwards. Was that a miracle? What does the orbit of the Moon around the Sun look like? How do you tell the difference between a waxing crescent Moon and a waning crescent Moon in San Francisco, Singapore and Sydney? If we have time, we will discuss which day the Sun rises earliest in San Francisco, Singapore and Sydney.
There are no prerequisites, and I hope that this talk will make you more conscious of the mathematics of the world around you, and give you knowledge that you will enjoy sharing with others for the rest of your life.
With the complex numbers well established, Gauss was convinced that there were no “hypercomplex” number systems with the same basic properties as the complex numbers. The search for hypercomplex numbers was on. In 1843 Hamilton discovered the quaternions, and soon after Graves and Cayley constructed the octaves.
We shall outline some results from the theory of real algebras (hypercomplex numbers) from Hamilton to 1958, when the question of the existence of finite dimensional real division algebras was finally settled.
At matematikkfaget har en lang historie bak seg, ble vi klar over allerede i våre skoledager når vi støtte på navn som Pythagoras, Euklid og Arkimedes. Men at historien går mye lengre tilbake enn til de gamle grekere, er det ikke så mange som vet. Og det er først i løpet av 1900-tallet historikerne for alvor ble klar over at man i høykulturene i bronsealderen kunne løse matematikkoppgaver som ligger langt utenfor all skolematematikk. I foredraget vil dette bli vist ved eksempler fra egyptiske papyrusruller og babylonske leirtavler, alt sammen fra årene mellom 2000 og 1500 f. Kr.
 Foto: Glen Larson
Foto: Glen Larson
In 1921 Johann Radon (yes, the one with the Radon transform) published a nice little theorem, the glorious future of which was difficult to foresee. It says that given a sequence of at least d+2 terms in Rd, it is possible to split the indices in two parts A and B in a particular way: Form the convex hull of the points with indices in A, and do the same with B. If the splitting is done in the right way, then the two convex hulls will have a non-empty intersection. The proof is a simple consequence of the fact that any set of n homogeneous linear equations in fewer than n unknowns, has a nontrivial solution. During the following 90 years the theorem has been generalized in many ways and it has given rise to difficult solved and still unsolved problems, dealt with by geometric, combinatorial and topological means. The talk will give a rough overview of the field and will fill in a few holes in Ziegler's accountpdf in Notices of the AMS April 2011.