
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.
(Juni 2003) Steinhaus' problem har funnet en løsning. Se addendum til annonseringen av Peter Lindqvists foredrag høsten 2001.
(Oktober 2003) Fra nå av holder Forumet til i vår nye «storstue», lunsjrommet i 13. etasje i Sentralbygg II.
i omvendt kronologisk rekkefølge
Hvor bør man sitte for å se en fotballkamp best mulig? Og hvorfor bør fotballsupportere ha kjennskap til «punktets potens» og andre geometriske temaer som forsvant ut av skolematematikken for en mannsalder siden? Og (for de unge) hva er «punktets potens» og de andre temaene som forsvant ut av skolematematikken for så lenge siden? I foredraget vil jeg forsøke å svare på disse spørsmålene og forklare sammenhengen mellom dem. Ingen spesielle forkunnskaper er nødvendig (men jeg vil driste meg til å derivere arcustangens!.)

«It was the happiest day of my life.»
Solitoner er i sin enkleste form lokaliserte overflatebølger (dvs som ikke brer seg utover med tiden) i et fluid. De ble oppdaget av den skotske ingeniøren Scott Russell i 1834, forble omdiskutert til Korteweg og de Vries utledet KdV-ligningen i 1895, og var deretter et kuriosum frem til midten av 1960-tallet da den moderne teorien for solitoner ble utviklet. Nå anvendes «solitonteori» i mange områder av naturvitenskap og teknologi i tillegg til at den har knyttet ulike matematiske disipliner sammen. Vi ser på den historiske utviklingen av denne teorien.
Den euklidiske geometrien tar for seg romlige problemer som involverer avstander og vinkler. Disse størrelsene skal bevares ved endring av posisjon, og man kan dermed kun tillate seg å translatere, rotere og (eventuelt) skalere sine studieobjekter, men på ingen måte deformere dem.
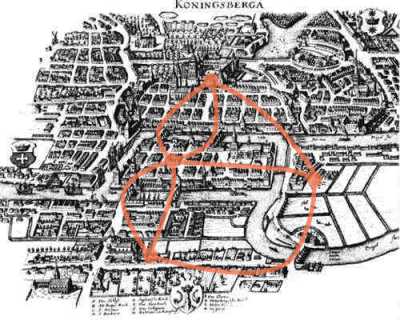
Problemet med Broene i Königsberg er, sett med våre øyne, trivielt, men bryter på en fundamental måte med den euklidiske geometrien. I klassisk geometri hadde man ikke begrepene til å formulere, og langt mindre løse, denne typen problemer. Eulers løsning av 1735 representerer et paradigmeskifte i og med at man studerer romlige problemer der avstand og vinkler ikke spiller noen rolle. Dette åpnet for muligheten til å ta fatt på en helt ny type problemer, og ledet frem mot det vi i dag kaller topologi.
Jeg skal presentere problemet med Broene i Königsberg, Eulers løsning av det generelle problemet som ligger bak, og til slutt anvende løsningen på Broene i Trondheim.

Dette er en fortelling om et matematisk «dyr» som ble skapt av John Butcher i 1972, og som så ble gjenoppdaget av Alain Connes (Fieldsmedaljevinner i 1983), Henri Moscovici og Dirk Kreimer i 1998. Det dreier seg om «Algebra of Rooted Trees» – ART.
Butchers hensikt var å analysere sammensetninger av numeriske metoder for løsning av differensialligninger. Connes og Moscovici studerte indeksteoremer i ikke-kommutativ geometri, og Kreimer var interessert i matematikken bak renormaliseringsmetoder i kvantefeltteori. Alle «snublet» over det samme objektet: Hopf-algebraen til grafer av rotfestede trær. Det hører med til sjeldenhetene at til de grader så forskjellige grener av matematikken har funnet et felles fundament!
I foredraget vil vi forsøke å forklare de grunnleggende begrepene og konstruksjonene på en elementær måte tilgjengelig for ikke-eksperter.
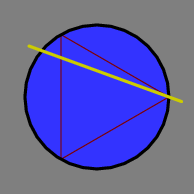
I 1889 formulerte J.L. Bertrand følgende problem: Kast et langt strå tilfeldig over en sirkel – gitt at strået krysser sirkelen – hva er sannsynligheten for at kordelengden er lengre enn sidene i sirkelens innskrevne likesidete trekant? Utsagnet – tilfeldig – er ikke presist definert, og ulike modeller for uniform tilfeldighet gir opphav til ulike løsninger. Det er problematisk.
Betyr det at problemet ikke kan evalueres sannsynlighetsteoretisk? Krever problemet eksperimentell utforskning? Ligger det informasjon i uuttrykte betingelser? E.T. Jaynes filosoferer over disse spørsmål i boka: Probability Theory - The logic of science (2003). Han foreslår også en vei ut av uføret.
Dagens tekst tar for seg dette temaet, og vi vil knytte noen kommentarer til det.

For
want of a nail, the shoe was lost;
For want of a shoe, the horse was lost;
For want of a horse, the rider was lost;
For want of a rider, the battle was lost;
For want of a battle; the kingdom was lost!
Både i det hverdagslige og innen vitenskapen er det kjent at små tilfeldigheter kan utløse store omveltninger. Frastøtende fikspunkter har skapt problemer i mange typer simuleringer. Likevel måtte mange teorier forkastes da det i siste halvdel av det 20. århundre ble oppdaget flere og flere kaotiske systemer. Det vil si systemer som var ustabile nesten overalt. Man måtte blant annet innse at man aldri vil kunne forutsi været eksakt.
Etterhvert som fraktaler ble satt i fokus gjennom 1970- og 80-tallet, vokste Mandelbrotmengden frem som selve symbolet på det nye feltet. De nydelige fargene og den uendelige kompleksiteten fascinerte mange. Jeg vil vise hvordan denne mengden konstrueres, og fortelle litt om hvilke egenskaper den har.
Et pythagoreisk trippel er som kjent et trippel av naturlige tall (a, b, c) hvor a2+b2=c2. Triplet er primitivt hvis a og b er uten felles faktor. Kjente eksempler på slike er for eksempel (3, 4, 5) og (5, 12, 13). Det finnes uendelig mange primitive pythagoreiske tripler, og allerede for over 3000 år siden (lenge før Pythagoras) kjente babylonerne en metode for hvordan de kunne finnes. Holme og flere andre historikere har antatt at det var «standardmetoden» de benyttet. Det er den som fortsatt finnes i de fleste tekster som behandler pythagoreiske tripler. I dette lille kåseriet vi se at det er mulig å benytte en geometrisk fremgangsmåte, som er mer visuell og vel så enkel. Siden babylonernes tenkning var utpreget geometrisk, er det ikke utenkelig at det var denne metoden de brukte. Med dette temaet som en passende oppvarming skal vi også se på noe jeg har kalt «pythagoreiske sirkler», og jeg skal presentere et «Pythagoreisk sirkelteorem».