
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.

I en ikke så alt for fjern fortid trodde vi mennesker at jorda var flat. Vi baserte kunnskapen på hva vi så rundt oss. Sannsynligvis ville de praktfulle bildene av den runde jorda, tatt fra verdensrommet, ha endret vår oppfatning – hvis vi hadde trodd på det vi så. Å studere jordoverflaten med utgangspunkt i hva man ser fra et punkt på den samme flaten kaller vi et lokalt perspektiv. Å se jorda utenifra, slik at vi faktisk kan se hele kloden, kaller vi et globalt perspektiv. Det globale perspektivet gir oss naturlig nok et mye bedre bilde, men er det mulig å få den samme kunnskapen ved et lokalt studium? Er det mulig å fastslå at jorda er rund, bare ved å studere overflaten lokalt?
Mange av de store resultatene i matematikk baserer seg på denne sammenhengen mellom lokale og globale egenskaper. Ved å samle sammen all tilgjengelig lokal kunnskap er vi i mange tilfeller i stand til å bestemme den globale strukturen. Gauss–Bonnet-teoremet er et eksempel på dette. Det sier at dersom vi kjenner krumningen av flaten i et hvert punkt, ja så kan vi si noe om den globale formen på flaten. Foredraget skal dreie seg om dette teoremet, men også om beslektede resultater som på samme måte relaterer lokale og globale strukturer.
The notion of a solution to a differential equation can be delicate, when the “solution” does not possess all the derivatives required by the equation. It is remarkable that the so-called viscosity solutions often work where all other notions fail. Yet, the modern definition of viscosity solutions is formulated in terms of the most basic rules in the infinitesimal calculus. The theory was developed by M.G. Crandall, L.C. Evans, P.-L. Lions (who won the Fields medal in 1994), H. Ishii, R. Jensen and others. The paper User's guide to viscosity solutions of second order partial differential equations (MathSciNet) has been cited hundreds of times according to MathSciNet. The field is rapidly expanding.
In particular, the theory applies to problems in optimal control, differential games and front propagation. In the talk this is not treated but, instead, the following examples will illustrate the viscosity theory:
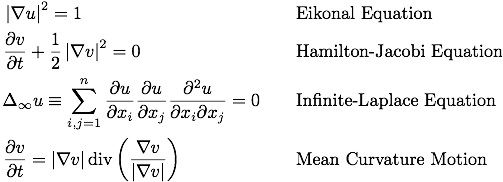
If time permits, some Calculus of Variations will be included.
Prerequisites: Infinitesimal calculus.
En trokoidekurve er en plan kurve som fremkommer ved at en sirkel A (av radius r) ruller uten glidning på en faststående sirkel B (av radius R). Et punkt P fast forbundet med den bevegelige sirkelen A beskriver da en trokoidekurve. Spesielt, dersom P ligger på omkretsen av A kaller vi kurvene sykloidekurver. (Gresk: τροχοειδής – hjulformet, κύκλος – sirkel.)
Første gang i historien at trokoidekurvene dukket opp (riktignok da beskrevet på en anderledes måte) var i oldtiden i forbindelse med grekernes beskrivelse av planetbanene som episykler (Apollonius, ~ 230 f. Kr.). I det 17nde århundre ble trokoidekurvene, og spesielt sykloidekurvene, inngående studert av de mest fremtredende matematikere (bl.a. Mersenne, Roberval, Huygens, Newton, Johann Bernoulli, Étienne Pascal (far,) Blaise Pascal (sønn) ). Av sykloidekurvene kjenner de fleste til kardioden (r=R og A ruller på utsiden av B), astroiden (R = 4r og A ruller på innsiden av B) og den vanlige sykloiden (R=∞, dvs. B er en rett linje).
Trokoidekurvene har en del bemerkelsesverdige geometriske egenskaper som har gjort at de har fått anvendelser innen mekanikk og teknologi. Dessuten opptrer de i forbindelse med lysrefleksjon som kaustikk-kurver, noe man kan observere i de mest dagligdagse situasjoner. Vi skal gi en presentasjon av alt dette, blant annet ved hjelp av animasjon.

Last year, 300 years after the death of Seki Takakazu, there was a celebration of this Japanese mathematician in Tokyo. This astonishing man was a samurai and regarded as Japan's most impressive mathematician from the middle ages. In later years Japanese mathematicians have tried to sort out what Seki and his contemporaries actually did and when they did it, in particular if they were the first to do it.
To me, however, there is a much more interesting angle that can be investigated. The important thing was that Japan was a totally closed country from 1633 to 1854. Foreigners were shut out, foreign books were banned and burned. The idea was that Japanese culture should be allowed to evolve quietly and undisturbed. And it did. So, what happened to mathematics in this extreme situation? Did they develop the same kind of mathematics, sooner or later, as elsewhere on this planet? In other words, is our mathematics the natural thing, doomed to come out the way it has?
In physics it is customary to describe a physical phenomenon by a system of functions and then, say: “They transform as follows”. The transformation rules then determine whether this is a function, a vector field or whatever it may be. This kind of talk can be pretty confusing to a mathematician, but what is meant is that one observer is observing a phenomenon wrt one coordinate system, another wrt another coordinate system, and the transformation rules determine what it is they are looking at and how the observations relate.
So if person A says: “This looks like a differentiable function to me”, and person B says: “I don't think so”, then of course there is trouble. Smooth manifolds provide a tool to avoid this kind of trouble, examples are spaces like e.g. S7 and R4, and a multitude of other examples as Lie Groups, homogeneous spaces, etc. In the talk I will explain that, surprisingly, in some cases there are essentially different ways that locally look just the same, but globally are essentially different. All relevant definitions will be given in the talk.
I analysens barndom var mange argumenter basert på regning med uendelig små eller uendelig store tall. Disse metodene ga raskt resultater, men de var befengt med en grunnleggende usikkerhet – ingen kunne definere slike tall eller skille dem fra de «vanlige» tallene. Infinitesimale metoder kom derfor i vanry, og ble erstattet med de grensebaserte begrepene vi bruker idag. Først på slutten av 1950-tallet utviklet Abraham Robinson metoder som gjorde at man kunne basere analysen på infinitesimaler på en trygg og konsistent måte. Jeg skal vise hvordan man kan bygge en tallinje med uendelig små og uendelig store elementer slik at den egner seg for matematisk analyse.
A keyhole view on continued fractions.


Gösta Mittag-Leffler (1846–1927), svensk matematikks største personlighet og en faglig gründer av internasjonalt format. Han glødet for sin vitenskap, og skapte ved sin lærergjerning det som i matematikkhistorien blir omtalt som Stockholm-skolen. Også for nordisk matematisk forskning var han en frontfigur. Han ble æresdoktor ved seks universiteter og æresmedlem i så godt som samtlige matematiske selskap verden over. I 1880-årene etablerte han Acta Mathematica og gjorde tidsskriftet til en ledende publiseringskanal for verdens matematikere, han fikk Sonja Kovalevsky til Stockholm og gjorde henne til verdens første kvinnelige matematikk-professor, og han fikk kong Oscar II interessert i matematikk.
Han hadde kontakt med de ledende matematikerne på den tiden: Weierstrass, Kronecker, Schwartz, Klein, Volterra, Poincaré, Appell, Picard, Hardy, Fields, etc, og selvfølgelig våre norske matematikere Lie, Sylow, Thue. Dessuten var han en entusiastisk beundrer av Abel.
Mittag-Lefflers storslåtte villa i Djursholm utenfor Stockholm huser i dag Institut Mittag-Leffler, et betydningsfullt internasjonalt sentrum for matematisk forskning.
Teorien for endelige grupper er verktøyet i studiet av symmetriforhold i Euklidsk geometri, i andre geometrier og i kombinatorikk. De «simple» endelige gruppene er byggeklossene i en dekomposisjon av de endelige gruppene. De simple endelige gruppene er klassifisert gjennom et «felttog» som involverte et stort antall matematikere fra 1950-tallet. To av de store «feltherrene» var Thompson og Tits som delte Abelprisen 2008. Opprydningsaksjoner pågår ennå.
De simple endelige gruppene kan organiseres i tre uendelige familier med rimelig tilgjengelige ensartede beskrivelser – pluss en familie på 26 «sporadiske» grupper som er spesielle på mange måter.
De første sporadiske gruppene ble funnet av Mathieu tidlig i gruppeteoriens utvikling (1861 og 1873). Det viste seg senere at de svarte til et høyst merkverdig symmetrisk objekt.
Først i 1965 fant Janko den neste sporadiske gruppen. Av de 26 danner 20 en egen underfamilie; de er undergrupper av den største, gjerne kalt «Monsteret».
Men Griess, med det første eksistensbeviset, fant at det dreide seg om «The Friendly Giant». Det finnes faktisk en «kjøkkenvei» som tillater oss en snarvisitt inn til noen av de 20 i «The Happy Family». Alle er invitert!