
Om Forum for
matematiske perler (og kuriositeter)
2001/2002 ·
2002/2003 ·
2003/2004 ·
2004/2005 ·
2005/2006 ·
2006/2007 ·
2007/2008 ·
2008/2009 ·
2009/2010 ·
2010/2011 ·
2011/2012 ·
2012/2013 ·
2013/2014 ·
2014/2015 ·
2015/2016 ·
2016/2017 ·
2017/2018 ·
2018/2019 ·
2019/2020 ·
2020/2021 ·
2021/2022 ·
2022→.

Et hovedtema i A Mathematician's Apology av G. H. Hardy (1877–1947) er skillet mellom «virkelig» matematikk, som er «ren» og totalt unyttig, og anvendt matematikk, som er kjedelig og triviell. Hardy innså neppe selv den mangfoldige ironien i at nettopp han målbar dette synet: Eksemplene er mange på at Hardys matematikk (tallteori og analyse) er blitt sentral for anvendelser, på måter som knapt kunne forutses på hans tid. Med fare for å virke pretensiøs, eventuelt under dekke av at forumet også kan omhandle matematiske kuriøsiteter, vil jeg beskrive en personlig erfaring med bruk av Hardyrom. Det dreier seg om et optimeringsproblem formulert av Johannes Skaar ved Institutt for elektronikk og telekommunikasjon. Problemet er knyttet til fenomenet «negativ brytning» og spørsmålet om man kan designe en «perfekt» linse, noe som har vært gjenstand for stor interesse i de senere år. Det teknologiske perspektivet er blant annet at løsningen av problemet kan gi eksakt informasjon om teoretiske grenser for oppløsningen på «nanonivå» i fremtidige datamaskiner. Jeg vil etter fattig evne beskrive den fysiske motivasjonen og dessuten hva Hardyrom er og hvordan antagelsen om kausalitet bringer dem inn i mange sammenhenger. Vi skal se at takket være noen små mirakler kan vårt problem løses eksakt. Løsningen involverer stort sett bare Hilbert-transformen og komplekse kvadratrøtter, men den er verken kjedelig eller triviell.
We all know that the circle encloses the largest area. That the circle is the solution to the isoperimetric problem was known to Zenodorus (200–140 BC?), whose lost work “On Isometric Figures” is mentioned by Pappus (290–350 AD?) and Theon. – I cannot resist mentioning the passage:
And when Zenodorus the Astronomer came down to Arcadia and was introduced to us, he asked us how to find a mirror surface such that when it is placed facing the sun the rays reflected from it meet at a point and thus cause burning – From Diocles' “On Burning Mirrors”
The first proof is due to Jacob Steiner 1841, who, strictly speaking, showed that no other curve will do. I will present one of Steiner's proofs. My footnote is the same problem in the metric
{|x1−y1|p+|x2−y2|p}1/p
The answer is elegant! Some interesting “sines” and “cosines” appear in the calculations.

Den imponerende oppblomstringen av gresk matematikk hadde sine røtter i tidligere epoker og sivilisasjoner. Vi skal starte med Eupalinos-tunnelen på Samos, via Thales komme til Pytagoras og pytagoreerne. Pytagoras' livshistorie forteller vi etter Jamblikos og andre fortellere, som lenge ble sett på med historikernes skepsis. Pytagoreernes mantra «alt er tall» støtte an mot geometrien da det ikke-målbares vesen ble avslørt. Fra pytagoreerne går veien videre til de store navnene i gresk og hellenistisk matematikk, frem til mordet på Hypatia i Alexandria i år 415 e. Kr. På denne tiden mistet herskerne (datidens politikere) interessen for matematikk og vitenskap. De var mer interessert i gladiatorkamper i vest og teologiske funderinger i øst. Da gikk det ikke så bra med romerriket. Kanskje vi kan lære noe av historien her også?

I Christiania våren 1825, før han la ut på sin to-årige utenlandsreise til Berlin og Paris, forfattet Abel et manuskript på fransk som han ga tittelen Sur la comparaison des fonctions transcendantes. Dette manuskriptet ble først offentlig kjent i og med Holmboes utgave fra 1839 av Abels samlede verker, altså ti år etter Abels død. Artikkelen kan betraktes som en forstudie til Abels berømte Pariseravhandling, som han la frem for l'Académie des Sciences i Paris 30 oktober 1826. Først i 1841 – etter mange viderverdigheter – ble Pariseravhandlingen trykt og publisert.
Abels tidlige manuskript innholder beviset for addisjonsteoremet i sin mest generelle form, og gir antydninger om hvordan han har tenkt å utvikle dette videre, noe Pariseravhandlingen tar opp i full bredde. Mer interessant for oss i denne sammenhengen er det at Abel illustrerer sitt addisjonsteorem ved å anvende det på helt elementære eksempler. Befridd som teoremet da er for de vanskelige undersøkelsene av de nye begrepene som det gir støtet til – eksempelvis genusbegrepet – fremtrer det på en konkret og begripbar måte.
Det er vanskelig å finne superlativer av høy nok valør når man skal karakterisere Abels addisjonsteorem – «matematisk perle» blir for spinkelt. Jakobi kalte det Die grösste mathematische Entdeckung unserer Zeit. I sin Traité d'Analyse fra 1901 uttrykte Picard det på denne måten:
Le théorème parait tout à fait élémentaire, et il n'y a peut-être pas, dans l'historie de la Science, de proposition aussi importante obtenue à l'aide de considérations aussi simples.
[Teoremet fremstår som helt elementært, og kanskje har det aldri forekommet i vitenskapshistorien et resultat som er så viktig, og som er oppnådd ved så enkle betraktninger.]
Foredraget tar sikte på å belyse og å konkretisere disse «enkle betraktningene» på bakgrunn av Abels tidlige manuskript. Det er sagt om Abels bevis at det ligner på løsningen av en øvingsoppgave i integralregningen. Utsagnet rommer en kjerne av sannhet, noe som bare øker fascinasjonen som addisjonsteoremet er omsluttet av. I foredraget vil vi poengtere bevisets elementære karakter, og forhåpentligvis overbevise tilhørerne om dets tilgjengelighet.

Tor Langbach er jurist og dommer i Trondheim tingrett, og er bl.a. kjent for å ha vært dommer i Orderudsaken. Han vil redegjøre for rettsvesenets problematiske forhold til sannsynlighet.
Hvor sannsynlig er det at Peder Ås voldtok Marte Kirkerud? Hvor sikker må dommeren være for å kunne dømme? Men om retten ikke finner sannsynligheten for Peders skyld sterk nok og derfor frifinner ham, hvordan kan det ha seg at retten likevel dømmer ham til å betale Marte erstatning for voldtekten? Og hvorfor får han kanskje etterpå erstatning fra staten? Hvordan kan en dommer være så sikker på at Peder er skyldig at han sperrer ham inne i fengsel inntil saken kommer opp, men deretter frifinner ham? Disse og lignende spørsmål vil dommeren forsøke å gi svar på!
... Cujus
rei demonstrationem mirabilem sane detexi. Hanc marginis
exiguitas non caperet.
(For denne påstanden har jeg oppdaget et vidunderlig bevis
som denne margen er for smal til å romme.)
Med denne bemerkningen fra 1637, skrevet av Fermat i margen på Bachets latinske oversettelse av grekeren Diophantus' ( ~ 250 e.kr.) samlede verker, ble legenden om Fermats Siste Teorem skapt. Fermat skrev ned beviset for kun ett av alle de teoremene i tallteori som han hevdet å ha bevist. Det var beviset for at ligningen x4+y4=z4 kun har trivielle løsninger i naturlige tall. Fermats Siste Teorem (kalt så fordi det var den eneste av Fermats påstander som forble uoppklart av Euler et al.) påstår som kjent at ligningen
xn+yn=zn
kun har trivielle løsninger i naturlige tall for alle n≥3.
Isolert sett er kjennskapet til korrektheten av Fermats påstand uvesentlig – ja, nærmest irrelevant – for matematikkens fremgang, akkurat som det faktum at mennesker landet på månen ikke førte til store landevinninger i vår kunnskap. Men bak sistnevnte bedrift lå store vitenskapelige og teknologiske fremskritt. På lignende måte er Wiles bevis i 1994 for Fermats Siste Teorem frukten av 350 års matematiske framskritt innen analyse og geometri, men spesielt innen algebra/tallteori. Det ubestridelige faktum at jakten på beviset for Fermats påstand var en viktig motivasjonskilde for mange av de matematikere som sto bak denne fremgangen, gjør at det alltid vil stå en egen glans omkring Fermats Siste Teorem.
Foredraget vil ha et nærmest kåseripreg, der vi spesielt skal stoppe ved følgende viktige milepæler:
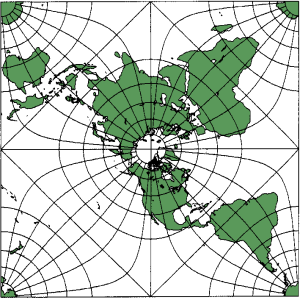
En noe uortodoks (men konform) kartprojeksjon.
En kartprojeksjon er en avbildning fra en del av jordoverflaten til et plant kart. Siden jorden er en (tilnærmet) kule og kart trykkes på flatt papir, er det umulig å lage en kartprojeksjon som er korrekt i ethvert henseende – for eksempel kan det ikke avbilde alle avstander i kartet med samme målestokk. Mercators projeksjon fra 1500-tallet er laget for navigatører: En rett linje i kartet svarer til en reiserute med samme kompasskurs hele veien. Denne projeksjonen er også konform, noe som er en nyttig og ettertraktet egenskap for kartprojeksjoner. (Den har også uheldige egenskaper, som at Grønland ser større ut enn Sør-Amerika for eksempel.) Konformitet vil si at vinkler bevares lokalt. Ekvivalent er at kartets lokale målestokk er den samme i alle retninger.
Carl Friedrich Gauss ga en meget elegant løsning til det generelle problemet om hvordan man kan karakterisere og konstruere konforme avbildninger fra en krum flate til planet, eller til en annen krum flate. Problemet var stilt som prisoppgave av det kongelige danske vitenskapsakademi i 1822. Som eksempler produserte han formler for Mercator-projeksjonen, ikke bare på en kule men også på en rotasjonsellipsoide, som jo er en bedre modell for jordkloden. Av spesiell interesse for oss er den såkalte transversale Mercatorprojeksjonen, som også har fått navnet Gauss–Krügers projeksjon. Denne brukes i definisjonen av UTM (Universal Transverse Mercator), som er det koordinatsystemet som er mest brukt i dag – og som nettopp definerer rutenettet i de populære 1:50000-kartene.